Aplikace Buckinghamovy věty pí

Další: Předchozí: Buckinghamova věta pí

Aplikace Buckinghamovy věty pí

Věta, kterou jsme uvedli, je velmi obecná, ale v žádném případě není omezena na mechaniku tekutin. Používá se v rozmanitých oborech, jako je botanika a společenské vědy, a na toto téma byly napsány knihy a svazky. Nepotřebujeme však mnoho teorie, abychom ji mohli použít. To, čím se budeme zabývat, je postup, jak tuto větu použít a dospět k nedimenzionálním číslům pro dané proudění.

1. Vyjmenujte všechny proměnné, kterými se proces řídí. Tyto proměnné by měly být na sobě nezávislé. Například by se neměla vybírat hustota, hmotnost a specifická hmotnost. Měla by stačit hustota a specifická hmotnost. Pro náš problém máme F, D, V, a . Máme n = 5.
2. Označte opakující se proměnné. V našem případě jsou to D, V a , takže k = 3 .
3. Rozhodněte, kolik je neurčitých čísel. V našem případě máme n – k = 2. Naše úloha má 2 nedimenzionální čísla, a .
4. Určete nedimenzionální čísla seskupením proměnných do n – k skupin tak, aby každá skupina měla všechny opakující se proměnné a jednu neopakující se proměnnou. Pro náš problém tedy máme

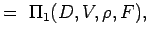
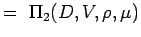
   		(5.).2)
   Let
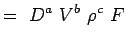
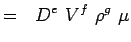
   		(5.3)

5. Nyní vyjádříme jednotlivé proměnné v jejich rozměrech. Použijme systém MLT, podle kterého mají proměnné pro našeproblémy následující dimenze.
   

   Proměnná	Rozměry
   F, síla	M L / T2 nebo M L T-2
   D, průměr:	L
   V, Rychlost	L/T nebo LT-1
   , Hustota:	M/L3 nebo ML-3
   , viskozita	ML-1T-1

   Při dosazení těchto rozměrů do rov. 5.2 máme

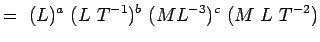
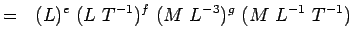
   		(5.4)
   nebo
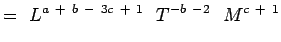
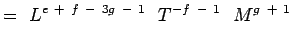
   		(5.5)

   Podle toho, že a jsou bezrozměrné, máme,

   a + b – 3c + 1 = 0; -b – 2 = 0, c + 1 = 0
   e + f – 3g – 1 = 0; -f – 1 = 0;g + 1 = 0	(5.6)

   Řešením rovnic získáme,

   a = -2, b = -2, c = -1
   e = -1, f = -1, g = -1	(5.7)

   Nyní se naše nerozměrná čísla stávají,

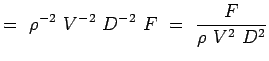
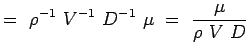
   		(5.8)

Tím jsme zjistili bezrozměrná čísla pro proudění, které nás zajímá, a to odpor kolem kruhového válce. Funkčnívztah mezi oběma čísly lze vyjádřit jako

Všimněte si však, že tvar členu , který jsme odvodili, je poněkud odlišný od toho, co jsme předpokládali na začátku. Pravá strana rovnice je ve skutečnosti inverzní Reynoldsovo číslo!“ To poukazuje na nevýhodu analýzy, že přesný funkční tvar mezi čísly nelze získat. Jakýkoli získaný koeficient nebo index nelze touto analýzou určit. Ten by měl být určen experimentálně nebo výpočtem. Ale protože čísla jsou nedimenzionální, můžeme vždy psát,

Další: Předchozí: Buckinghamova věta o čísle pí

(c) Aerospace, Mechanical & Mechatronic Engg. 2005
University of Sydney