Magnitudový digitální komparátor je kombinační obvod, který porovnává dvě digitální nebo binární čísla s cílem zjistit, zda je jedno binární číslo rovno, menší nebo větší než druhé binární číslo. Logicky navrhneme obvod, pro který budeme mít dva vstupy, jeden pro A a druhý pro B, a tři výstupní svorky, jednu pro podmínku A > B, jednu pro podmínku A = B a jednu pro podmínku A <B.
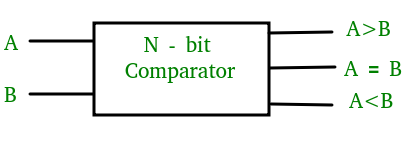
Jednobitový komparátor velikosti –
Komparátor používaný k porovnávání dvou bitů se nazývá jednobitový komparátor. Skládá se ze dvou vstupů, každý pro dvě jednobitová čísla, a tří výstupů pro generování menší než, rovno a větší než mezi dvěma binárními čísly.
Pravdivostní tabulka pro jednobitový komparátor je uvedena níže:
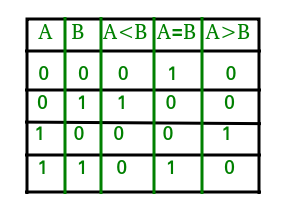
Z výše uvedené pravdivostní tabulky lze logické výrazy pro jednotlivé výstupy vyjádřit následovně:
A>B: AB'A<B: A'BA=B: A'B' + AB
Z výše uvedených výrazů lze odvodit následující vzorec:

Pomocí těchto logických výrazů můžeme realizovat logický obvod pro tento komparátor, jak je uvedeno níže:
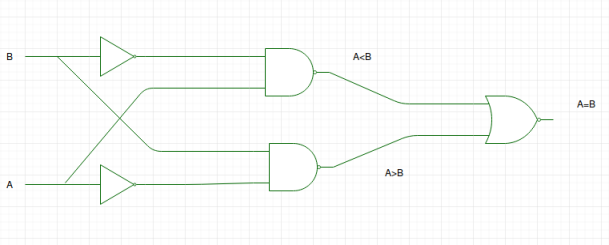
Logické schéma je chybné
2-bitový komparátor velikosti –
Komparátor používaný k porovnávání dvou binárních čísel, z nichž každé má dva bity, se nazývá 2-bitový komparátor velikosti. Skládá se ze čtyř vstupů a tří výstupů pro generování menšího než, rovného a většího než mezi dvěma binárními čísly.
Pravdivostní tabulka pro 2bitový komparátor je uvedena níže:
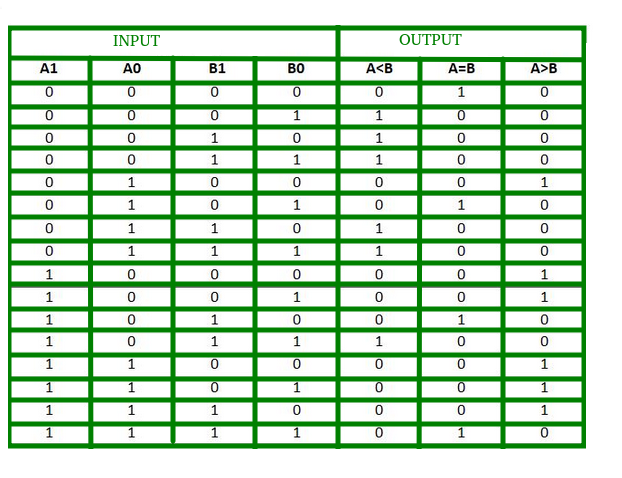
Z výše uvedené pravdivostní tabulky lze K-mapu pro každý výstup sestavit následovně:



Z výše uvedených K-map lze logické výrazy pro každý výstup vyjádřit následovně:
A>B:A1B1' + A0B1'B0' + A1A0B0'A=B: A1'A0'B1'B0' + A1'A0B1'B0 + A1A0B1B0 + A1A0'B1B0' : A1'B1' (A0'B0' + A0B0) + A1B1 (A0B0 + A0'B0') : (A0B0 + A0'B0') (A1B1 + A1'B1') : (A0 Ex-Nor B0) (A1 Ex-Nor B1)A<B:A1'B1 + A0'B1B0 + A1'A0'B0
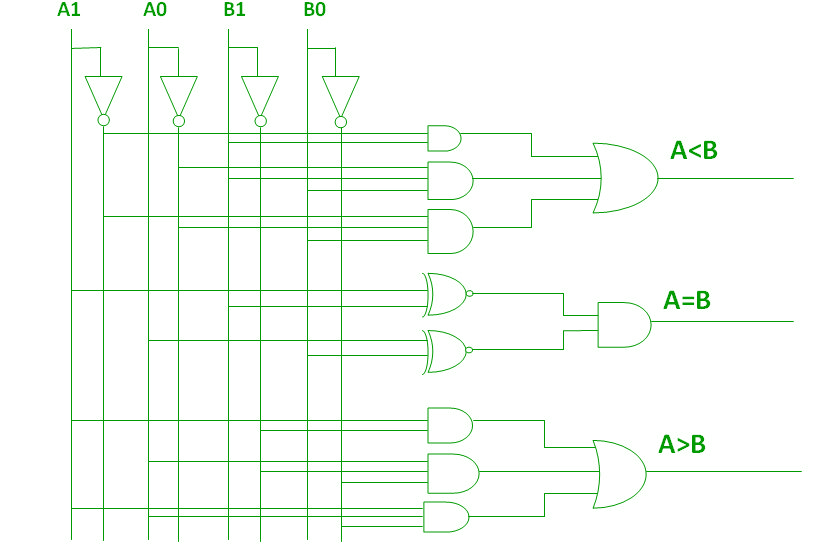
Pomocí těchto logických výrazů můžeme realizovat logický obvod pro tento komparátor, jak je uvedeno níže:
4-bitový komparátor velikosti –
Komparátor používaný k porovnávání dvou binárních čísel, z nichž každé má čtyři bity, se nazývá 4-bitový komparátor velikosti. Skládá se z osmi vstupů, každý pro dvě čtyřbitová čísla, a tří výstupů pro generování menší než, rovno a větší než mezi dvěma binárními čísly.
Ve 4bitovém komparátoru může být podmínka A>B možná v následujících čtyřech případech:
- Jestliže A3 = 1 a B3 = 0
- Jestliže A3 = B3 a A2 = 1 a B2 = 0
- Jestliže A3 = B3, A2 = B2 a A1 = 1 a B1 = 0
- Jestliže A3 = B3, A2 = B2, A1 = B1 a A0 = 1 a B0 = 0
Podobně lze podmínku pro A<B splnit v následujících čtyřech případech:
- Jestliže A3 = 0 a B3 = 1
- Jestliže A3 = B3 a A2 = 0 a B2 = 1
- Jestliže A3 = B3, A2 = B2 a A1 = 0 a B1 = 1
- Jestliže A3 = B3, A2 = B2, A1 = B1 a A0 = 0 a B0 = 1
Podmínka A=B je možná pouze tehdy, když se všechny jednotlivé bity jednoho čísla přesně shodují s odpovídajícími bity jiného čísla.
Z výše uvedených tvrzení lze logické výrazy pro jednotlivé výstupy vyjádřit následovně:
AA, 831331 r: (A3 EioNor 33)A2132′ a (A3 Ex-Nor 133) (A2 Ex-Nor 132)A131′ a (A3 Ex-Nor 33) (A2 ENor132) (Al Ex-Nor 31)A01301
,13: A3’03 a (A3 Ex-Nor 33)A211:12 a (A3 Ex-Nor 83) (A2 Ex-Nor 132)Ar131 a (A3 Ex-Nor 33) (A2 Ex-Nor32) (Al Ex-Nor 131)A0N30
A=B: (A3 Ex-Nor B3) (A2 Ex-Nor 82) (Al Ex-Nor BI) (AO Ex-Nor BO)
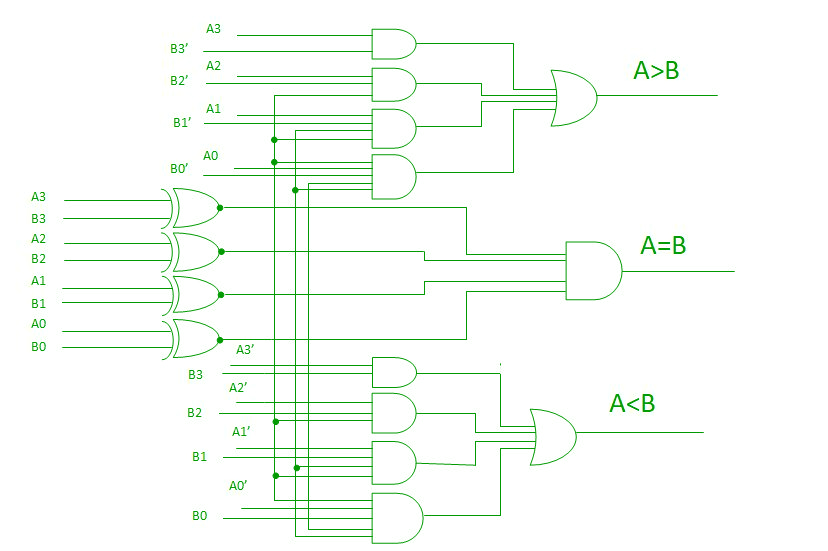
Pomocí těchto logických výrazů můžeme realizovat logický obvod pro tento komparátor, jak je uvedeno níže:
Kaskádový komparátor –
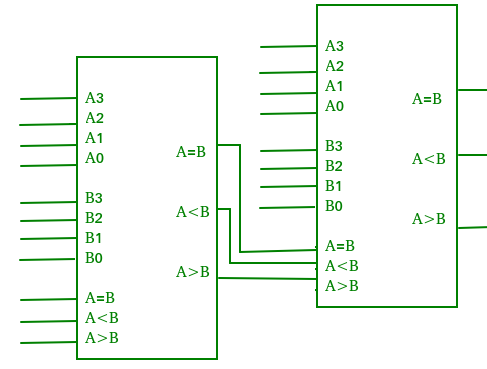
Kaskádový komparátor, který provádí porovnávací operaci na více než čtyři bity kaskádováním dvou nebo více 4bitových komparátorů, se nazývá kaskádový komparátor. Při kaskádování dvou komparátorů se výstupy komparátoru nižšího řádu připojí na odpovídající vstupy komparátoru vyššího řádu.
Použití komparátorů –
- Komparátory se používají v centrálních procesorech (CPU) a mikrokontrolérech (MCU).
- Ty se používají v řídicích aplikacích, v nichž se binární čísla reprezentující fyzikální veličiny, jako je teplota, poloha atd. se porovnávají s referenční hodnotou.
- Komparátory se používají také jako procesní regulátory a pro řízení servomotorů.
- Používají se v aplikacích pro ověřování hesel a v biometrických aplikacích.
.
