Před několika lety napsal Scott Fortmann-Roe skvělou esej s názvem „Pochopení kompromisu mezi odchylkou a odchylkou“
Jak se datová věda mění v uznávanou profesi s vlastním souborem nástrojů, postupů, pracovních postupů atd, se často zdá, že je kladen menší důraz na statistické procesy ve prospěch zajímavějších aspektů (dvojici příkladů diskusí naleznete zde a zde).
Pojmové definice
Ačkoli toto bude sloužit jako přehled Scottovy eseje, kterou si můžete přečíst pro další podrobnosti a matematické postřehy, začneme doslovnými definicemi Fortmann-Roe, které jsou pro tento článek stěžejní:
Chybou způsobenou zkreslením: Chybu způsobenou zkreslením chápeme jako rozdíl mezi očekávanou (nebo průměrnou) předpovědí našeho modelu a správnou hodnotou, kterou se snažíme předpovědět. Samozřejmě máte pouze jeden model, takže mluvit o očekávaných nebo průměrných hodnotách předpovědi se může zdát poněkud zvláštní. Představte si však, že byste celý proces tvorby modelu mohli opakovat vícekrát: pokaždé, když shromáždíte nová data a provedete novou analýzu, vytvoříte nový model. Vzhledem k náhodnosti v podkladových souborech dat budou mít výsledné modely určitý rozsah předpovědí. Zkreslení měří, jak daleko jsou obecně předpovědi těchto modelů od správné hodnoty.
Chybovost způsobená rozptylem: Chyba způsobená rozptylem se bere jako variabilita předpovědi modelu pro daný datový bod. Opět si představte, že celý proces sestavování modelu můžete opakovat vícekrát. Rozptyl je to, jak moc se předpovědi pro daný bod liší mezi různými realizacemi modelu.
V podstatě je odchylka to, jak moc jsou předpovědi modelu vzdáleny od správnosti, zatímco rozptyl je míra, do jaké se tyto předpovědi liší mezi iteracemi modelu.
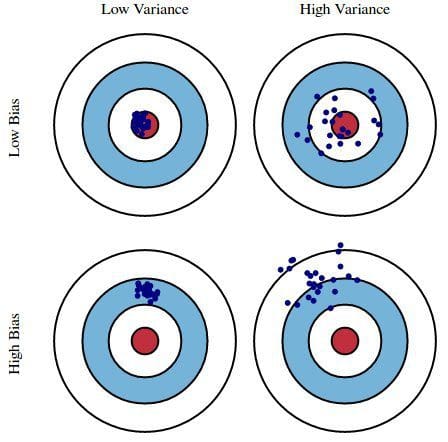
Obr. 1: Grafické znázornění zkreslení a rozptylu
Z knihy Understanding the Bias-Variance Tradeoff, autor Scott Fortmann-Roe.
Diskuse
Na příkladu jednoduchého chybného průzkumu prezidentských voleb jsou pak chyby v průzkumu vysvětleny dvojí optikou zkreslení a rozptylu: výběr účastníků průzkumu z telefonního seznamu je zdrojem zkreslení; malá velikost vzorku je zdrojem rozptylu; minimalizace celkové chyby modelu závisí na vyvážení chyb zkreslení a rozptylu.
Fortmann-Roe se dále zabývá těmito otázkami ve vztahu k jedinému algoritmu: k-nejbližšímu sousedovi. Poté uvádí několik klíčových otázek, na které je třeba myslet při řízení zkreslení a rozptylu, včetně technik opětovného výběru vzorků, asymptotických vlastností algoritmů a jejich vlivu na chyby zkreslení a rozptylu a boje s vlastními předpoklady vůči datům i jejich modelování.
Esej končí tvrzením, že ve své podstatě jsou tyto dva pojmy úzce spojeny s nadměrným i nedostatečným přizpůsobením. Podle mého názoru je zde nejdůležitější bod:
Jak se do modelu přidává stále více parametrů, složitost modelu roste a rozptyl se stává naším hlavním zájmem, zatímco zkreslení neustále klesá. Například čím více polynomických členů se přidá do lineární regrese, tím větší bude složitost výsledného modelu. Jinými slovy, bias má zápornou derivaci prvního řádu v závislosti na složitosti modelu, zatímco variance má kladný sklon.

Obr. 2: Bias a variance přispívající k celkové chybě
Z knihy Understanding the Bias-Variance Tradeoff, autor Scott Fortmann-Roe.
Fortmann-Roe končí část o nadměrném a nedostatečném přizpůsobení poukazem na další ze svých skvělých esejů (Přesné měření chyby predikce modelu) a poté přechází k velmi souhlasnému doporučení, že „opatření založená na opakovaném výběru, jako je křížová validace, by měla být upřednostňována před teoretickými opatřeními, jako je Aikakeho informační kritérium“.
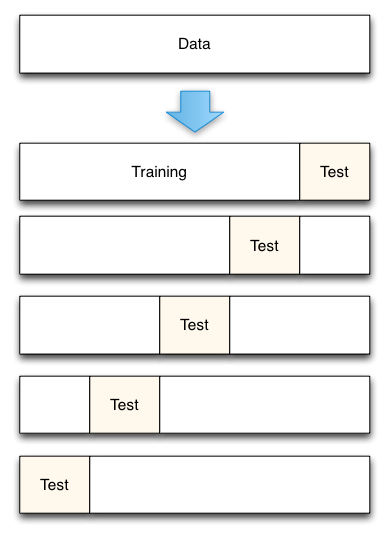
Obr. 3: Pětinásobné rozdělení dat křížovou validací
Z článku Přesné měření chyby predikce modelu, autor Scott Fortmann-Roe.
Při křížové validaci je samozřejmě důležitým rozhodnutím počet záhybů, které se použijí (k-násobná křížová validace, že?), hodnota k.
Při křížové validaci je důležitým rozhodnutím počet záhybů, které se použijí. Čím nižší hodnota, tím větší zkreslení odhadů chyb a tím menší rozptyl. Naopak, pokud je hodnota k rovna počtu instancí, odhad chyby je pak velmi málo zkreslený, ale má možnost vysokého rozptylu. Je zřejmé, že kompromis mezi zkreslením a rozptylem je důležité pochopit i u těch nejrutinnějších metod statistického vyhodnocování, jako je k-násobná křížová validace.
Naneštěstí se také zdá, že křížová validace občas ztrácí v moderní době datové vědy svůj půvab, ale to je diskuse na jindy.
Doporučuji přečíst si celou esej Scotta Fortmanna-Roea o kompromisu mezi zkreslením a odchylkou a také jeho článek o měření chyby predikce modelu.
Související:
- Velká data, biblické kódy a Bonferroni
- Data science of Variable Selection: Přehled
- Datové soubory nad algoritmy
