Úvod :
Kosinová podobnost se používá k určení podobnosti mezi dokumenty nebo vektory. Matematicky měří kosinus úhlu mezi dvěma vektory promítnutými do vícerozměrného prostoru. k dispozici jsou i další techniky měření podobnosti, například euklidovská vzdálenost nebo manhattanská vzdálenost, ale my se zde budeme věnovat kosinové podobnosti a kosinové vzdálenosti.
Vztah mezi kosinovou podobností a kosinovou vzdáleností lze definovat takto:
- Podobnost se zmenšuje, když se zvětšuje vzdálenost mezi dvěma vektory

2. Podobnost se zvětšuje, když se zmenšuje vzdálenost mezi dvěma vektory.

Kosinová podobnost a kosinová vzdálenost:
Kosinová podobnost říká, že ke zjištění podobnosti mezi dvěma body nebo vektory musíme najít úhel mezi nimi.
Vzorec pro zjištění kosinové podobnosti a vzdálenosti je následující:


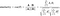
Tady A=bod P1,B=bod P2 (v našem příkladu)
Podívejme se na různé hodnoty Cos Θ pro pochopení kosinové podobnosti a kosinové vzdálenosti mezi dvěma datovými body(vektory) P1 & P2 s ohledem na dvě osy X a Y.
Následující obrázek má tyto případy.
Případ 1: Když je úhel mezi body P1 & P2 45 stupňů, pak
kosinová podobnost= Cos 45 = 0.525
Případ 2: Když jsou dva body P1 & P2 od sebe vzdáleny a úhel mezi body je 90 Stupňů pak
cosine_similarity= Cos 90 = 0
Případ 3: Když jsou dva body P1 & P2 od sebe vzdáleny a úhel mezi body je 90 Stupňů pak
cosine_similarity= Cos 90 = 0: Když jsou dva body P1 & P2 velmi blízko sebe a leží na stejné ose a úhel mezi body je 0 stupňů, pak
cosine_similarity= Cos 0 = 1

Následující obrázek má další tři případy.
Případ 4: Když body P1 & P2 leží proti sobě a úhel mezi body je 180 Stupňů, pak
kosin/podobnost= Cos 180 = -1
Případ 5: Když úhel mezi body P1 & P2 je 270 Stupňů, pak
kosin/podobnost= Cos 270 = 0
Případ 6: Když úhel mezi body P1 & P2 je 270 Stupňů, pak
kosin/podobnost= Cos 270 = 0
: Když je úhel mezi body P1 & P2 360 Stupňů, pak
cosine_similarity= Cos 360 = 1

Přejděme tyto hodnoty jednotlivých výše diskutovaných úhlů a podívejme se na kosinusovou vzdálenost mezi dvěma body.
1 – Cosine_Similarity=Cosine_Distance
Případ 1: Když Cos 45 stupňů
Nasaďme hodnoty ve výše uvedeném vzorci .
1-0.525= Cosine_Vzdálenost
0.475 =Kosin_Vzdálenost
Případ 2: Když Cos 90 Stupeň
1-0= Kosin_Vzdálenost
1 =Kosin_Vzdálenost
Případ 3: Když Cos 0 Stupeň
1-1= Kosin_Vzdálenost
0 =Kosin_Vzdálenost
Případ 4: Když Cos 0 Stupeň
1-1= Kosin_Vzdálenost
:
1-(-1)=Kosin_Vzdálenost
2 =Kosin_Vzdálenost
Případ 5: Když Cos 270 Stupeň
1-0= Kosin_Vzdálenost
1 =Kosin_Vzdálenost
Případ 6:
1-1= Cosine_Distance
0 =Cosine_Distance
Jasně vidíme, že když je vzdálenost menší, podobnost je větší(body jsou blízko sebe) a vzdálenost je větší ,dva body jsou nepodobné (daleko od sebe)
Kosinová podobnost a kosinová vzdálenost se hojně využívá v doporučovacích systémech k doporučování produktů uživatelům na základě toho, co se jim líbí a nelíbí.
Několik příkladů, kde se to používá, jsou webové stránky jako Amazon, Flipkart k doporučování položek zákazníkům pro personalizované zážitky, hodnocení a doporučování filmů atd.
Závěr : Doufám, že jste nyní jasně pochopili matematiku, která stojí za výpočtem kosinové podobnosti a kosinové vzdálenosti, a její použití.
Doufám, že se vám můj článek líbil. prosím, stiskněte tlačítko Clap 👏 (50krát), abyste mě motivovali k dalšímu psaní.
Chcete se připojit :
Odkaz : https://www.linkedin.com/in/anjani-kumar-9b969a39/
Pokud se vám mé příspěvky zde na Médiu líbí a přáli byste si, abych v této práci pokračoval, zvažte, zda mě podpořit na patreonu
.
