Link state routing je technika, při které každý směrovač sdílí znalosti o svém okolí s každým dalším směrovačem v internetové síti.
Tři klíče k pochopení algoritmu Link State Routing:
- Znalosti o okolí: Namísto odesílání své směrovací tabulky odesílá směrovač pouze informace o svém okolí. Směrovač vysílá ostatním směrovačům své identity a náklady na přímo připojené spoje.
- Zaplavování: Každý směrovač odesílá informace všem ostatním směrovačům v internetové síti kromě svých sousedů. Tento proces je znám jako Flooding. Každý směrovač, který přijme paket, odešle jeho kopie všem svým sousedům. Nakonec každý směrovač obdrží kopii stejné informace.
- Sdílení informací: Směrovač odesílá informace každému jinému směrovači pouze tehdy, když dojde ke změně informací.
Směrování ve stavu linky má dvě fáze:
Spolehlivé zaplavení
- Počáteční stav: Každý uzel zná náklady svých sousedů.
- Konečný stav: Každý uzel zná celý graf.
Výpočet trasy
Každý uzel používá Dijkstrův algoritmus na grafu k výpočtu optimálních tras do všech uzlů.
- Směrovací algoritmus Link state je také známý jako Dijkstrův algoritmus, který se používá k nalezení nejkratší cesty z jednoho uzlu do každého jiného uzlu v síti.
- Dijkstrův algoritmus je iterační a má tu vlastnost, že po k-té iteraci algoritmu jsou dobře známy cesty s nejmenšími náklady pro k cílových uzlů.
Popišme si některé notace:
- c( i , j): Pokud uzly i a j nejsou přímo propojeny, pak c(i , j) = ∞.
- D(v): Určuje náklady na cestu ze zdrojového kódu do cílového bodu v, která má v současné době nejmenší náklady.
- P(v):
- N: Je to celkový počet uzlů, které jsou v síti k dispozici.
Algoritmus
InitializationN = {A} // A is a root node.for all nodes vif v adjacent to Athen D(v) = c(A,v)else D(v) = infinityloopfind w not in N such that D(w) is a minimum.Add w to NUpdate D(v) for all v adjacent to w and not in N:D(v) = min(D(v) , D(w) + c(w,v))Until all nodes in N
V uvedeném algoritmu následuje inicializační krok a smyčka. Počet opakování smyčky je roven celkovému počtu uzlů, které jsou v síti k dispozici.
Pochopíme to prostřednictvím příkladu:
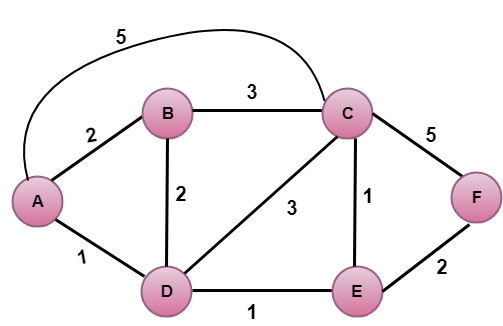
Na výše uvedeném obrázku je zdrojový vrchol A.
Krok 1:
První krok je inicializační krok. Aktuálně známé cesty nejmenších nákladů z A k jeho přímo připojeným sousedům, B, C, D, jsou 2,5,1 v tomto pořadí. Náklady z A do B jsou nastaveny na 2, z A do D jsou nastaveny na 1 a z A do C jsou nastaveny na 5. Náklady z A do E a F jsou nastaveny na nekonečno, protože nejsou přímo připojeny k A.
| Krok | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
Krok 2:
Ve výše uvedené tabulce vidíme, že vrchol D obsahuje cestu s nejmenšími náklady v kroku 1. Proto je přidán do N. Nyní musíme určit nejméně nákladovou cestu přes vrchol D.
a) Výpočet nejkratší cesty z A do B
b) Výpočet nejkratší cesty z A do C
c) Výpočet nejkratší cesty z A do E
Poznámka: Vrchol D nemá přímou vazbu na vrchol E. Proto je hodnota D(F) nekonečná.
| Krok | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
| 2 | AD | 2,A | 4,D | 2,D | ∞ |
Krok 3:
Ve výše uvedené tabulce vidíme, že E i B mají v kroku 2 cestu s nejmenšími náklady. Uvažujme vrchol E. Nyní určíme nejméně nákladnou cestu zbývajících vrcholů přes E.
a) Výpočet nejkratší cesty z A do B.
b) Výpočet nejkratší cesty z A do C.
c) Výpočet nejkratší cesty z A do F.
| Krok | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | |
| 3 | ADE | 2,A | 3,E | 4,E |
Krok 4:
V uvedené tabulce vidíme, že vrchol B má v kroku 3 cestu s nejmenšími náklady. Proto jej přidáme do N. Nyní určíme nejméně nákladnou cestu zbývajících vrcholů přes B.
a) Výpočet nejkratší cesty z A do C.
b) Výpočet nejkratší cesty z A do F.
| Krok | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | |
| 3 | ADE | 2,A | 3,E | 4,E | ||
| 4 | ADEB | 3,E | 4,E |
Krok 5:
V uvedené tabulce vidíme, že vrchol C má v kroku 4 cestu s nejmenšími náklady. Proto jej přidáme do N. Nyní určíme nejméně nákladnou cestu zbývajících vrcholů přes C.
a) Výpočet nejkratší cesty z A do F.
| Krok | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | |
|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | ||
| 3 | ADE | 2,A | 3,E | 4,E | |||
| 4 | ADEB | 3,E | 4,E | ||||
| 5 | ADEBC | 4,E |
Závěrečná tabulka:
| Krok | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | |
|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | ||
| 3 | ADE | 2,A | 3,E | 4,E | |||
| 4 | ADEB | 3,E | 4,E | ||||
| 5 | ADEBC | 4,E | |||||
| 6 | ADEBCF |
Nevýhoda:
Silný provoz vzniká při směrování ve stavu Line kvůli Flooding. Flooding může způsobit nekonečné zacyklení, tento problém lze vyřešit použitím pole Time-to-leave
.
