Tato teorie se někdy nazývá teorií „statického“ přílivu a odlivu, která se poprvé objevila ve slavných Principiích Isaaca Newtona. Poté, co Newton a další, kteří ho následovali, identifikovali síly způsobující příliv a odliv, představili hypotetický globální oceán, který je s těmito silami ve statické rovnováze – rovnováha vyžaduje, aby Zemi pokrýval aprolovaný sféroid vody. „Prolátovitý“ znamená, že dotyčná koule byla protažena podél přímky spojující dva póly; v tomto případě ne zeměpisné póly, ale póly v linii s nebeským tělesem (Měsícem nebo Sluncem), které způsobují deformaci hypotetické oceánské koule. Podíváme-li se znovu na grafiku znázorňující tažné síly v předchozím modulu, můžeme si snadno představit, jak se voda sbíhá k těmto pólům a vytváří dvojí „slapovou výduť“ – termín, který je stále velmi populární v moderních učebnicích.
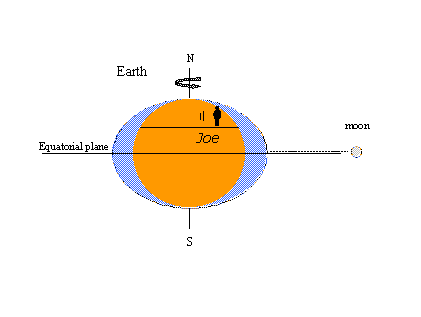
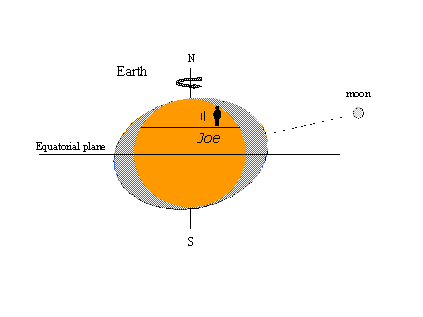
Důvodem popularity teorie rovnováhy – přinejmenším konceptu slapových výduti – je to, že je snadné vysvětlit některé dobře známé slapové jevy pomocí obrázků. Na tom vlevo dole rotuje imaginární pozorovatel jménem Joe se Zemí a setkává se se statickými výčnělky v podobě přílivu a odlivu. kdykoli Měsíc protne Joeův místní poledník, je svědkem přílivu. O dvanáct lunárních hodin později, když Měsíc překročí opačnýemeridian na druhé straně Země, je příliv znovu. Během jednoho lunárního dne trvajícího 24 hodin a 50 minut hodinového (slunečního) času nastanou dva přílivy a dva odlivy. Na obrázku vpravo Měsíc postoupil na své dráze kolem Země do polohy severně od rovníku (severní deklinace). Statické výčnělky se pohybují tak, aby zůstaly v jedné linii s Měsícem, a Joe se nyní setkává s denní nerovnoměrností přílivu a odlivu (po sobě jdoucí přílivy a odlivy nestejné výšky). Maximální měsíční deklinace severně nebo jižně od rovníku vytváří tropické přílivy a odlivy; přílivy a odlivy vyskytující se, když je Měsíc na rovníku, se nazývají rovníkové přílivy a odlivy. tropicko-rovníkové přílivy a odlivy se opakují dvakrát v intervalu 27 1/3 dne – tropický měsíc pokrývá jeden úplný cyklus v měsíční deklinaci. Všechna tato pozorování jsou v souladu s teorií rovnováhy.
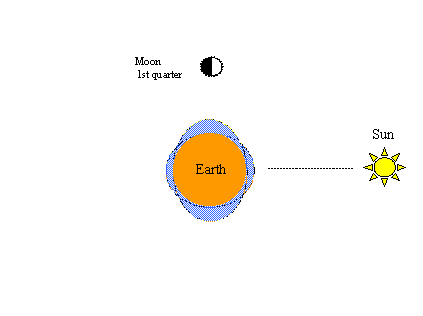
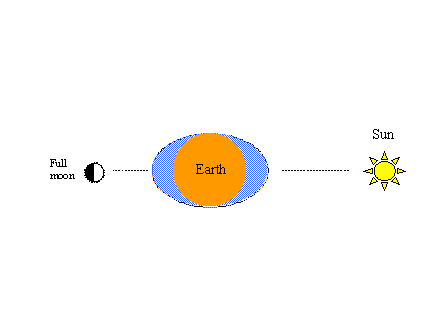
Dalším jevem, který lze tímto způsobem snadno prokázat, je známý cyklus jarní-nepodzimní. Sluneční gravitace také vytváří dvojici přílivových výčnělků v hypotetickém oceánu. Když jsou tažné síly Slunce aMěsíce v souladu, vznikají jarní přílivy většího rozsahu (vyšší maxima a nižší minima)jak ukazuje obrázek vlevo dole. Stejně jako na předchozích obrázcích, když Měsíc dokončí další půlcyklus na své dráze – tentokrát od úplňku do novu – dojde opět k jarnímu přílivu a odlivu.
Níže uvedený obrázek vpravo znázorňuje neapolskou část jarně-neapolského cyklu; tj. když je Měsíc v první čtvrtině (nebo třetí čtvrtině) tohoto cyklu, měsíční a sluneční tažné síly jsou zcela mimo linii, mají tendenci se vzájemně vyvažovat a vzniká neapolský příliv menšího rozsahu (nižší výšky a vyšší minima). Dva jarní-neapo cykly (dva jarní a dva neapo) jsou dokončeny za 29 a půl dne, což je stejná doba, jakou potřebuje Měsíc k dokončení jednoho úplného oběhu Země vůči Slunci.
Další aspekty pozorovaného přílivu a odlivu v souladu s rovnovážnou teorií zahrnují perigeoapo cyklus. Ten vyplývá ze skutečnosti, že oběžná dráha Měsíce kolem Země opisuje spíše elipsu než kruh. Perigeální přílivy většího rozsahu se vyskytují v perigeu Měsíce, kdy je Měsíc nejblíže k Zemi, a apogeální přílivy menšího rozsahu se vyskytují v apogeu Měsíce, kdy je Měsíc na své eliptické dráze nejdále od Země. Perigeoapogeální cyklus trvá přibližně 27 a půl dne.
Ačkoli teorie rovnováhy skvěle vysvětluje cyklické slapové jevy a doby opakování spojené s mnoha z nich, je příkladem modelu ideálního chování – něčeho, co funguje pro zamýšlený účel, i když se nemusí ve všech případech držet pravdy. Tyto případy nemusíme hledat daleko. Země je jen zčásti pokryta svými vodami, pevninské masy brání tomu, aby cokoli, co by se podobalo přílivu, putovalo zcela kolem ní, a pozorování skutečných přílivů a odlivů ukazují, že nereagují okamžitě na přílivotvorné síly Měsíce aSlunce, jak teorie vyžaduje.
