Směrodatná odchylka je číslo, které nám říká
do jaké míry se od sebe liší množina čísel.Směrodatná odchylka se může pohybovat od 0 do nekonečna. Směrodatná odchylka 0 znamená, že seznam čísel je stejný – neleží od sebe vůbec v žádné míře.
Směrodatná odchylka – příklad
Pět uchazečů podstoupilo test IQ jako součást žádosti o zaměstnání. Jejich výsledky ve třech složkách IQ jsou uvedeny níže.
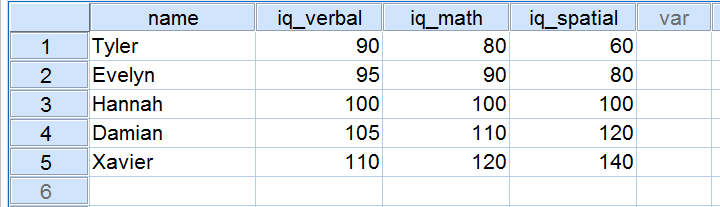
Podívejme se nyní blíže na výsledky ve třech složkách IQ. Všimněte si, že všechny tři mají průměr 100 u našich 5 uchazečů. Nicméně skóre v iq_verbal leží blíže u sebe než skóre v iq_math. Kromě toho leží skóre v iq_spatial dále od sebe než skóre v prvních dvou složkách. Přesný rozsah, v jakém od sebe leží určitý počet skóre, lze vyjádřit číslem. Toto číslo se nazývá směrodatná odchylka.
Standardní odchylka – výsledky
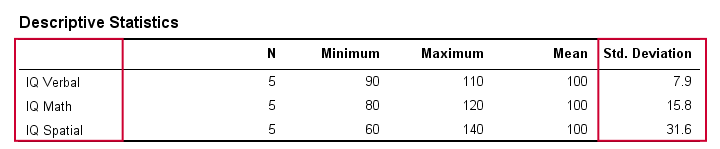
V reálném životě samozřejmě vizuálně nekontrolujeme hrubé skóre, abychom zjistili, jak daleko od sebe leží. Místo toho si je jednoduše necháme vypočítat nějakým softwarem (o tom později). Následující tabulka ukazuje směrodatné odchylky a některé další statistiky pro naše údaje o IQ. Všimněte si, že směrodatné odchylky potvrzují vzorec, který jsme viděli v surových datech.
Standardní odchylka a histogram
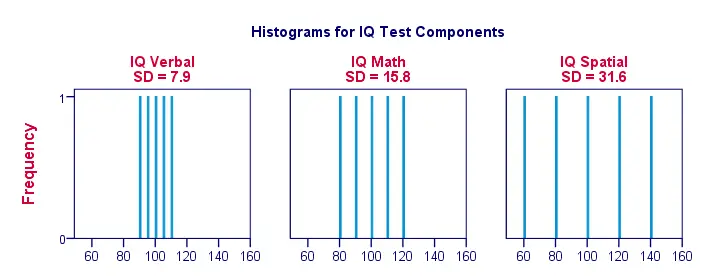
Pravda, udělejme si věci trochu názornější. Na obrázku níže jsou zobrazeny směrodatné odchylky a histogramy pro naše skóre IQ. Všimněte si, že každý sloupec představuje skóre 1 uchazeče v 1 složce IQ. Opět vidíme, že směrodatné odchylky ukazují, do jaké míry jsou skóre od sebe vzdálena.
Směrodatná odchylka – další histogramy
Pokud vizualizujeme data jen na několika pozorováních jako na předchozím obrázku, snadno uvidíme jasný obraz. Pro realističtější příklad níže uvedeme histogramy pro 1 000 pozorování. Důležité je, že tyto histogramy mají stejná měřítka; u každého histogramu odpovídá jeden centimetr na ose x přibližně 40 „bodům složky IQ“.
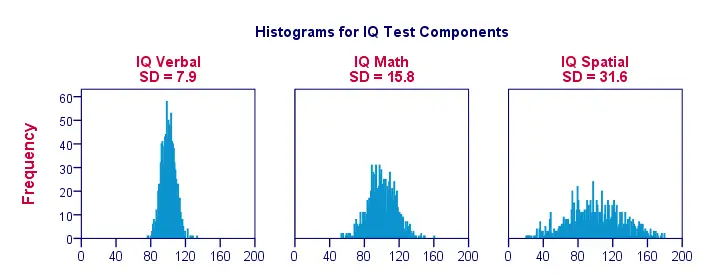
Všimněte si, jak histogramy umožňují hrubý odhad směrodatných odchylek. ‚Širší‘ histogramy naznačují větší směrodatné odchylky; skóre (osa x) leží dále od sebe. Protože všechny histogramy mají stejnou plochu (odpovídající 1 000 pozorování), jsou větší směrodatné odchylky spojeny také s „nižšími“ histogramy.
Standardní odchylka – populační vzorec
Jak tedy váš software počítá směrodatné odchylky? No, základní vzorec je
$$\sigma = \sqrt{\frac{\sum(X – \mu)^2}{N}}$$
kde
- \(X\) označuje každé samostatné číslo;
- \(\mu\) označuje průměr všech čísel a
- \(\sum\) označuje součet.
Slovy: směrodatná odchylka je odmocnina z průměrného čtvercového rozdílu mezi každým jednotlivým číslem a průměrem těchto čísel.
Důležité je, že tento vzorec předpokládá, že vaše data obsahují celou sledovanou populaci (proto „populační vzorec“). Pokud vaše data obsahují pouze vzorek z cílové populace, viz níže.
Populační vzorec – software
Tento vzorec můžete použít v listech Google, OpenOffice a Excelu zadáním =STDEVP(...) do buňky. Mezi závorky zadejte čísla, nad kterými chcete vypočítat směrodatnou odchylku, a stiskněte klávesu Enter. Obrázek níže ilustruje tuto myšlenku.
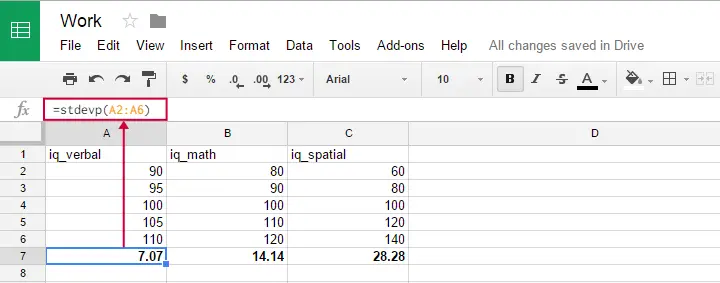
Je zvláštní, že vzorec pro směrodatnou odchylku populace v SPSS zřejmě neexistuje.
Standardní odchylka – vzorec pro vzorek
Teď něco náročného: pokud jsou vaše data (přibližně) prostým náhodným vzorkem z nějaké (mnohem) větší populace, pak předchozí vzorec bude v této populaci systematicky podhodnocovat směrodatnou odchylku. Nezkreslený odhad směrodatné odchylky populace získáme pomocí
$$S_x = \sqrt{\frac{\sum(X – \overline{X})^2}{N -1}}$$
Co se týče výpočtů, velký rozdíl oproti prvnímu vzorci je v tom, že dělíme \(n -1\) místo \(n\). Dělení menším číslem vede k (o něco) většímu výsledku. Tím se přesně kompenzuje výše zmíněné podhodnocení. Pro velké velikosti vzorků však mají oba vzorce prakticky totožné výsledky.
V GoogleSheets, Open Office a MS Excel používá funkce STDEV tento druhý vzorec. Je to také (jediný) vzorec pro směrodatnou odchylku implementovaný v programu SPSS.
Směrodatná odchylka a rozptyl
Druhým číslem, které vyjadřuje, jak daleko od sebe leží soubor čísel, je rozptyl. Rozptyl je čtverec směrodatné odchylky. Z toho vyplývá, že podobně jako směrodatná odchylka má rozptyl populační i výběrový vzorec.
V zásadě je trapné, že dvě různé statistiky v podstatě vyjadřují stejnou vlastnost souboru čísel. Proč prostě nezavrhneme rozptyl ve prospěch směrodatné odchylky (nebo naopak)? Základní odpovědí je, že směrodatná odchylka má v některých situacích žádanější vlastnosti a rozptyl v jiných.
.
