Anwendung des Satzes von Buckingham Pi

Nächste: Bedeutung der nichtdimensionalen Zahlen Up: Buckingham Pi Theorem Previous: Buckingham Pi Theorem

Anwendung des Buckingham Pi Theorems

Das von uns aufgestellte Theorem ist sehr allgemein, aber keineswegs auf die Strömungsmechanik beschränkt. Es wird in so unterschiedlichen Bereichen wie der Botanik und den Sozialwissenschaften angewandt, und es wurden Bücher und Bände zu diesem Thema geschrieben. Aber wir brauchen nicht viel Theorie, um es anwenden zu können. Was wir betrachten werden, ist ein Verfahren, um das Theorem anzuwenden und zu dimensionslosen Zahlen für eine gegebene Strömung zu gelangen.

1. Listen Sie alle Variablen auf, die den Prozess bestimmen. Diese Variablen sollten voneinander unabhängig sein. Zum Beispiel sollte man nicht Dichte, Schwerkraft und spezifisches Gewicht wählen. Dichte und spezifisches Gewicht sollten ausreichen. Für unser Problem haben wir F, D, V, und . Wir haben n = 5.
2. Markieren Sie die sich wiederholenden Variablen. In unserem Fall sind das D, V und , was k = 3 ergibt.
3. Bestimme, wie viele dimensionslose Zahlen es gibt. In unserem Fall haben wir n – k = 2. Unser Problem hat 2 nichtdimensionale Zahlen, und .
4. Bestimme die nichtdimensionalen Zahlen, indem du die Variablen in n – k Gruppen gruppierst, so dass jede Gruppe alle sich wiederholenden Variablen und eine sich nicht wiederholende Variable hat. So haben wir für unser Problem

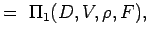
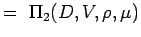
   		(5.2)
   Let
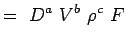
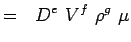
   		(5.3)

5. Nun drücken wir jede Variable in Form ihrer Dimensionen aus. Verwenden wir das MLT-System, nach dem die Variablen für unser Problem die folgenden Dimensionen haben.
   

   Variable	Dimensionen
   F, Kraft	M L / T2 oder M L T-2
   D, Durchmesser:	L
   V, Velocity	L/T oder LT-1
   , Density:	M/L3 oder ML-3
   , Viskosität	ML-1T-1

   Setzt man diese Größen in Gln. 5.2 einsetzen, erhalten wir

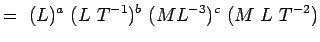
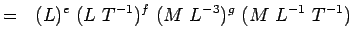
   		(5.4)
   Oder
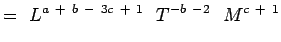
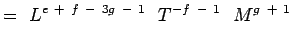
   		(5.5)

   Nachdem und dimensionslos sind, haben wir,

   a + b – 3c + 1 = 0; -b – 2 = 0, c + 1 = 0
   e + f – 3g – 1 = 0; -f – 1 = 0;g + 1 = 0	(5.6)

   Auflösen der Gleichungen ergibt,

   a = -2, b = -2, c = -1
   e = -1, f = -1, g = -1	(5.7)

   Nun werden unsere nichtdimensionalen Zahlen,

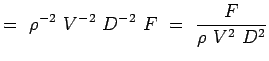
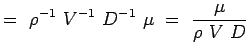
   		(5.8)

Damit haben wir die dimensionslosen Zahlen für die interessierende Strömung, nämlich den Widerstand um einen Kreiszylinder, gefunden. Die funktionale Beziehung zwischen den beiden Zahlen kann wie folgt ausgedrückt werden:

Aber beachten Sie, dass die Form des Terms , den wir abgeleitet haben, etwas anders ist, als wir zu Beginn angenommen haben. Die rechte Seite der Gleichung ist in Wirklichkeit der Kehrwert der Reynolds-Zahl! Dies weist auf den Nachteil der Analyse hin, dass die exakte funktionale Form zwischen den Zahlen nicht erhalten werden kann. Jeder ermittelte Koeffizient oder Index kann durch diese Analyse nicht bestimmt werden. Dies sollte durch Experimente oder Berechnungen ermittelt werden. Aber da die Zahlen nichtdimensional sind, können wir immer schreiben,

Weiter: Bedeutung der nichtdimensionalen Zahlen Up: Buckingham Pi Theorem Previous: Buckingham Pi Theorem

(c) Aerospace, Mechanical & Mechatronic Engg. 2005
University of Sydney