Um Brüche zu addieren (oder zu subtrahieren), müssen die Nenner der Brüche gleich sein.
Gleiche Nenner
Wenn die Nenner gleich sind, wird die Summe der Brüche berechnet, indem man die Zähler addiert und den Nenner behält.
Beispiel:
Wir addieren 4/7 und 3/7:
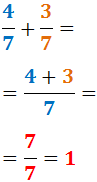 Auf die gleiche Weise wird die Subtraktion von Brüchen mit gleichen Nennern berechnet, indem man die Zähler subtrahiert und den Nenner behält.
Auf die gleiche Weise wird die Subtraktion von Brüchen mit gleichen Nennern berechnet, indem man die Zähler subtrahiert und den Nenner behält.
Beispiel:
Wir subtrahieren 4/7 und 3/7:
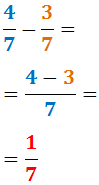
Unterschiedliche Nenner
Wenn die Nenner unterschiedlich sind, müssen wir ein wenig operieren, um die Brüche in äquivalente Brüche umzuwandeln, damit sie den gleichen Nenner haben.
Erläutern wir das Vorgehen beim Berechnen der Summe
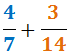
1. Wir berechnen das kleinste gemeinsame Vielfache der Nenner:
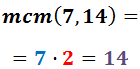
2. In den Nenner jedes Bruchs schreibt man das kleinste gemeinsame Vielfache, das man erhält:
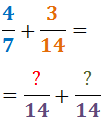
3. In den Zähler eines jeden Bruchs schreiben wir das Ergebnis der Division des kleinsten gemeinsamen Vielfachen (des neuen Nenners) durch den ursprünglichen Nenner und dessen Multiplikation mit dem ursprünglichen Zähler: Der ursprüngliche Nenner des ersten Bruchs war 7 und der ursprüngliche Zähler war 4:
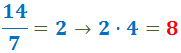
Der anfängliche Nenner des zweiten Bruches war 14 und der anfängliche Zähler war 3:
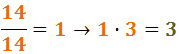
Damit haben wir die Summe von zwei Brüchen mit gleichem Nenner:
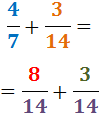
4. Wir addieren die Brüche:
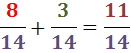
Um zu subtrahieren, folgen wir den gleichen Schritten, aber am Ende, anstatt die Brüche zu addieren, subtrahieren wir sie.
Ressourcen für Brüche:
- Begriff des Bruches
- Vereinfachung von Brüchen
- Äquivalente Brüche (1)
- Äquivalente Brüche (2)
- Addieren und Subtrahieren von Brüchen
- Multiplizieren und Dividieren. Brüche
- Brüche, die Dezimalzahlen erzeugen
- Gemischte Brüche
- Prozentsatzprobleme
- Interaktive Bruchübungen
- Operationen mit Brüchen
