Einführung :
Die Kosinusähnlichkeit wird zur Bestimmung der Ähnlichkeit zwischen Dokumenten oder Vektoren verwendet. Mathematisch gesehen misst sie den Kosinus des Winkels zwischen zwei Vektoren, die in einen mehrdimensionalen Raum projiziert werden. es gibt noch andere Verfahren zur Messung der Ähnlichkeit, wie z.B. die Euklidische Distanz oder die Manhattan-Distanz, aber wir werden uns hier auf die Kosinusähnlichkeit und die Kosinusdistanz konzentrieren.
Die Beziehung zwischen Cosinus-Ähnlichkeit und Cosinus-Abstand kann wie folgt definiert werden.
- Die Ähnlichkeit nimmt ab, wenn der Abstand zwischen zwei Vektoren zunimmt

2. Die Ähnlichkeit nimmt zu, wenn der Abstand zwischen zwei Vektoren abnimmt.

Cosinus-Ähnlichkeit und Cosinus-Abstand:
Die Cosinus-Ähnlichkeit besagt, dass man, um die Ähnlichkeit zwischen zwei Punkten oder Vektoren zu finden, den Winkel zwischen ihnen finden muss.
Die Formel zur Bestimmung der Cosinus-Ähnlichkeit und des Abstands lautet wie folgt:


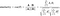
Hier A=Punkt P1,B=Punkt P2 (in unserem Beispiel)
Lassen Sie uns die verschiedenen Werte von Cos Θ betrachten, um die Kosinusähnlichkeit und den Kosinusabstand zwischen zwei Datenpunkten (Vektoren) P1 & P2 unter Berücksichtigung der beiden Achsen X und Y zu verstehen.
Das folgende Bild zeigt die Fälle.
Fall 1: Wenn der Winkel zwischen den Punkten P1 & P2 45 Grad beträgt, dann
ist Cosinusähnlichkeit= Cos 45 = 0.525
Fall 2: Wenn zwei Punkte P1 & P2 weit voneinander entfernt sind und der Winkel zwischen den Punkten 90 Grad beträgt, dann
kosinus_ähnlichkeit= Cos 90 = 0
Fall 3: Wenn zwei Punkte P1 & P2 sehr nahe beieinander liegen und der Winkel zwischen den Punkten 0 Grad beträgt, dann
Kosinusähnlichkeit= Cos 0 = 1

Nachfolgendes Bild zeigt die nächsten drei Fälle.
Fall 4: Wenn die Punkte P1 & P2 einander gegenüberliegen und der Winkel zwischen den Punkten 180 Grad beträgt, dann
cosine_similarity= Cos 180 = -1
Fall 5: Wenn der Winkel zwischen den Punkten P1 & P2 270 Grad beträgt, dann
cosine_similarity= Cos 270 = 0
Fall 6: Wenn der Winkel zwischen den Punkten P1 & P2 360 Grad beträgt, dann
cosine_similarity= Cos 360 = 1

Lassen Sie uns diese Werte für jeden der oben besprochenen Winkel eingeben und den Cosinusabstand zwischen zwei Punkten betrachten.
1 – Cosinus_Ähnlichkeit=Cosinus_Abstand
Fall 1: Wenn Cos 45 Grad
Lassen Sie uns die Werte in obiger Formel ersetzen.
1-0.525= Cosinus_Distanz
0.475 =Kosinusabstand
Fall 2: Wenn Cos 90 Grad
1-0= Kosinusabstand
1 =Kosinusabstand
Fall 3: Wenn Cos 0 Grad
1-1= Kosinusabstand
0 =Kosinusabstand
Fall 4: Wenn Cos 180 Grad
1-(-1)= Cosinus_Distanz
2 =Cosinus_Distanz
Fall 5: Wenn Cos 270 Grad
1-0= Cosinus_Distanz
1 =Cosinus_Distanz
Fall 6: Wenn Cos 360 Grad
1-1= Cosinus_Distanz
0 =Cosinus_Distanz
Wir können deutlich sehen, dass, wenn der Abstand geringer ist, die Ähnlichkeit größer ist (die Punkte liegen nahe beieinander), und wenn der Abstand größer ist, zwei Punkte unähnlich sind (weit voneinander entfernt)
Cosinusähnlichkeit und Cosinusdistanz werden häufig in Empfehlungssystemen verwendet, um den Benutzern Produkte auf der Grundlage ihrer Vorlieben und Abneigungen zu empfehlen.
Einige Beispiele, bei denen dies verwendet wird, sind Websites wie Amazon, Flipkart, um den Kunden Artikel für personalisierte Erfahrungen zu empfehlen, Filmbewertungen und Empfehlungen usw.
Abschluss: Ich hoffe, du hast jetzt ein klares Verständnis der Mathematik hinter der Berechnung der Kosinusähnlichkeit und der Kosinusdistanz und ihrer Verwendung.
Hoffe, dass dir mein Artikel gefällt.Bitte klatsche 👏(50 Mal), um mich zu motivieren, weiter zu schreiben.
Willst du dich mit mir verbinden :
Linked In : https://www.linkedin.com/in/anjani-kumar-9b969a39/
Wenn dir meine Beiträge hier auf Medium gefallen und du dir wünschst, dass ich diese Arbeit fortsetze, kannst du mich auf Patreon unterstützen
