Die Schätzung von Zeit, Aufwand und Kosten ist einer der kritischsten Teile des Projektmanagements. Dies liegt an der grundlegenden Bedeutung dieser Schätzungen für die gesamte Projektplanung und insbesondere für den Umfang, den Zeitplan und die Kostenbasis. Eine der im PMI Project Management Body of Knowledge (PMBOK 6. Auflage, Kap. 6.4, 7.2) empfohlenen Schätztechniken ist die Dreipunktschätzung, die mit der Dreiecks-, Beta- oder PERT-Verteilung verwendet wird. In diesem Artikel werden diese Methoden vorgestellt.
Was ist die Drei-Punkte-Schätzung?
Die Drei-Punkte-Schätzung ist ein einfacher, aber nützlicher Ansatz zur Schätzung der Zeit oder der Kosten von Arbeitselementen. Nach der PMI-Methodik wird sie in den Prozessgruppen „Estimate Activity Duration“ und „Estimate Costs“ eingesetzt. Die Technik umfasst drei verschiedene Schätzungen, die in der Regel von Fachexperten eingeholt werden:
- Optimistische Schätzung,
- Pessimistische Schätzung,
- wahrscheinlichste Schätzung.
Die optimistische Schätzung ist der erwartete Arbeits- oder Zeitaufwand für die Durchführung einer Aktivität unter der Annahme, dass keine Hindernisse auftreten und alles glatt läuft. Sie stellt das sogenannte Best-Case-Szenario dar. Der pessimistische Punkt basiert auf der Annahme, dass das Gegenteil der Fall ist – er stellt das Worst-Case-Szenario dar. Obwohl sich beide Schätzungen auf die Extrempunkte des Spektrums der zu erwartenden Ergebnisse beziehen, sollen die Schätzungen einigermaßen realistisch sein.
Der dritte Punkt spiegelt den wahrscheinlichsten Fall wider, es ist die Schätzung von Arbeit oder Zeit, die als am realistischsten angesehen wird. Man könnte versucht sein, einfach den Mittelwert zwischen dem optimistischen und dem pessimistischen Punkt zu verwenden, ohne weiter darüber nachzudenken. Dies ist jedoch in vielen Fällen nicht sinnvoll. In der Praxis lohnt es sich in der Regel, diesen wahrscheinlichsten Schätzwert richtig zu bestimmen, analog zu den anderen Schätzpunkten.
Das Ergebnis der Drei-Punkte-Schätzung ist eine so genannte Dreiecksverteilung von Zeitwerten oder Kostenbeträgen, die sich aus den drei Schätzwerten zusammensetzt (siehe Abbildung unten).
Was ist PERT?
PERT steht für Program Evaluation and Review Technique und wurde in den 1950er Jahren von der US-Marine als fortschrittliches Projektplanungs- und Managementsystem entwickelt (Quelle: Heldman, PMP Study guide, Kap. 4).
Eine andere, nicht ganz ernst gemeinte Entstehungsgeschichte wurde einst von einem anonymen Autor in der Zeitschrift des PMI veröffentlicht (Link; Quelle: Anonymous (1975). PERT-the hoax of the century. Project Management Quarterly, 6(3), 22-23).
In PMI-Projekten wird PERT in erster Linie als ergänzende Technik zur Methode des kritischen Pfades für die Terminplanung von Aktivitäten verwendet. Sie kann aber auch auf eigenständige Schätzungen von Arbeitspositionen und Aktivitäten angewendet werden.
Die so genannte PERT-Verteilung nutzt die mit der Drei-Punkte-Schätztechnik ermittelten Werte. Sie kann grundsätzlich für alle Planungsebenen eingesetzt werden, von Aktivitäten bis hin zu ganzen Projekten. Die richtige Granularität für eine sinnvolle Schätzung zu finden, kann jedoch einige kritische und konzeptionelle Überlegungen erfordern.
Die PERT-Methode impliziert eine Übergewichtung der „wahrscheinlichsten“ Schätzung. Sie wandelt die Drei-Punkte-Schätzung in eine glockenförmige Kurve um und ermöglicht es, Wahrscheinlichkeiten für Bereiche von Erwartungswerten zu bestimmen.
Was sind die Unterschiede zwischen der Dreiecksverteilung und der PERT-Verteilung von Drei-Punkte-Schätzungen?
Während die Dreiecksverteilung nur die drei geschätzten Punkte berücksichtigt, ermöglicht die PERT-Methode die Umwandlung der Drei-Punkte-Schätzung in eine glockenförmige, nahezu normalverteilte Kurve und kann somit zur Berechnung von Wahrscheinlichkeiten für Bereiche von Erwartungswerten verwendet werden.
Das folgende Diagramm veranschaulicht die Unterschiede zwischen der PERT-Verteilung, der Dreiecksverteilung und der Darstellung der Dreipunktschätzung als Normalverteilung.
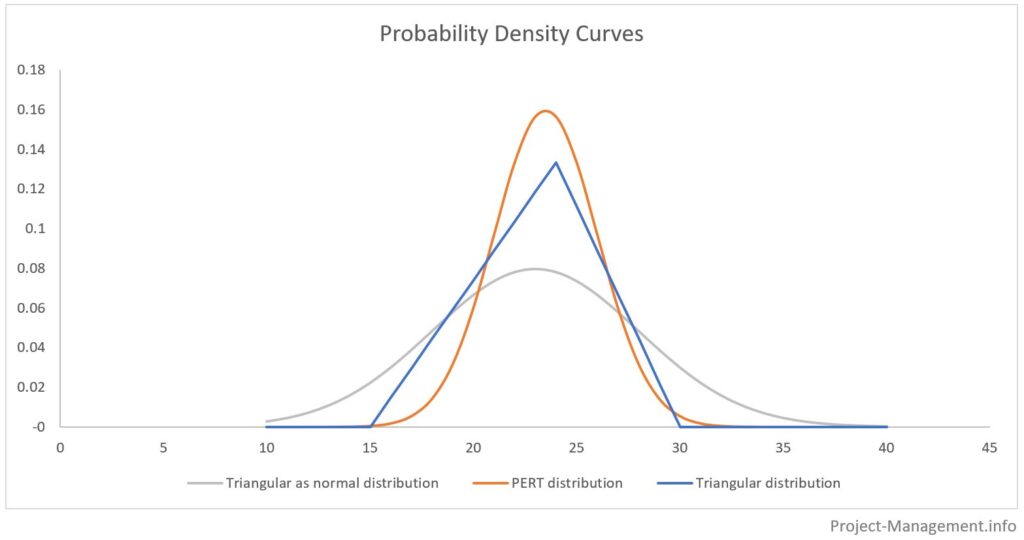
Die Flächen unter den Wahrscheinlichkeitsverteilungskurven stellen die kumulativen Wahrscheinlichkeiten der jeweiligen Schätzbereiche dar. Typischerweise werden diese Bereiche mit dem Erwartungswert +/- Standardabweichung multipliziert mit 1, 2 und 3 bestimmt. Dies wird in der folgenden Abbildung veranschaulicht:
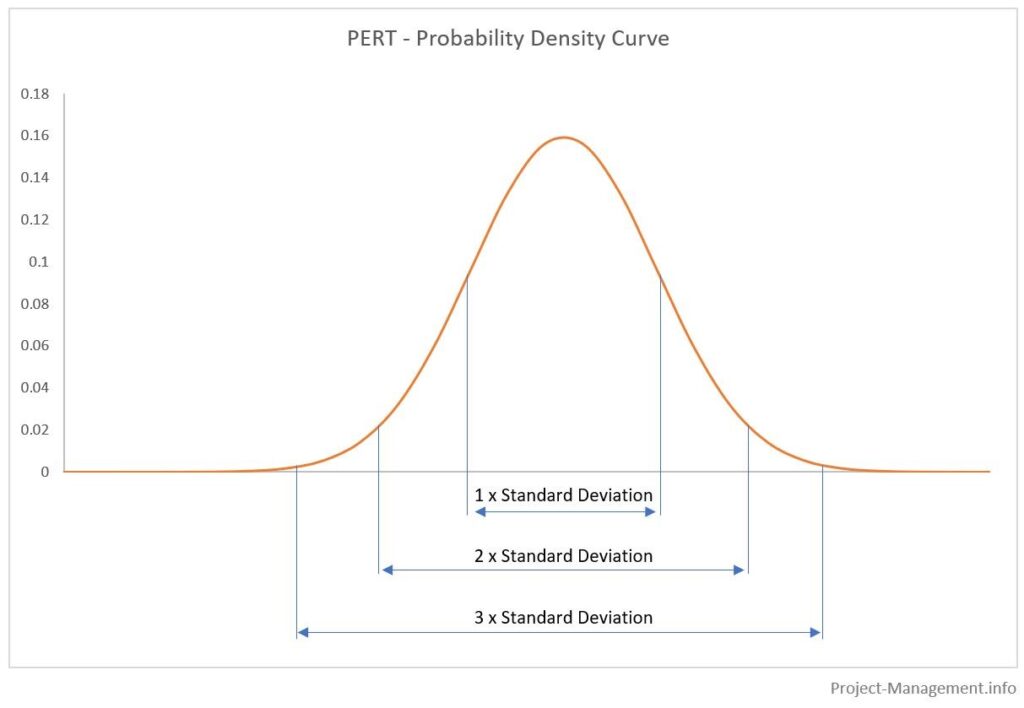
Die resultierenden Wahrscheinlichkeiten (ca.) sind
- 68,3% für 1 Standardabweichung,
- 95.5% für 2 Standardabweichungen,
- 99,7% für 3 Standardabweichungen.
Das für die PMP-Prüfung erforderliche Wissen beschränkt sich auf die Berechnung der erwarteten Schätzungen und die Kenntnis der verschiedenen Wahrscheinlichkeiten (Quelle). Daher werden wir in diesem Artikel nicht auf die statistischen Details und Hintergründe eingehen – diese finden Sie auf Riskamp.
Benutzen Sie diesen Rechner, um die Drei-Punkte-Schätzungen und PERT zu bestimmen.
Wie wird die Drei-Punkte-Schätzung berechnet?
Die Dreiecksverteilung
Die einfache, aber häufig verwendete Berechnung beinhaltet den Durchschnitt oder Mittelwert der 3 geschätzten Werte. Die Formel dieser Dreiecksverteilung lautet:
E =(O + M + P) / 3
wobei:
E = Erwarteter Zeit- oder Kostenaufwand,
O = Optimistische Schätzung,
M = Wahrscheinlichste Schätzung,
P = Pessimistische Schätzung.
Das PMBOK verwendet t(E), t(O), t(M) und t(P) als Variablen für Zeitschätzungen und c(E), c(O), c(M) und c(P).
Die Gewichtung der einzelnen Schätzungen in dieser Gleichung ist gleich. Somit hat der „wahrscheinlichste“ Fall keinen größeren Einfluss auf die endgültige Schätzung als die beiden weniger wahrscheinlichen Schätzungen. Dies unterscheidet sich von der Betaverteilungsmethode.
Die PERT-Beta-Verteilung
Die PERT-Beta-Verteilung berücksichtigt, dass der „wahrscheinlichste“ Fall wahrscheinlicher ist, was sich in einem Multiplikator für diese Schätzung niederschlägt. Die PMI-Methodik schlägt diese Berechnung als Alternative zur Dreiecksverteilung für Kostenschätzungen vor (wir sind jedoch der Meinung, dass sie auch für Zeitschätzungen verwendet werden kann).
Bei dieser Methode erhält die wahrscheinlichste Schätzung einen Multiplikator von 4, während der Gesamtdivisor auf 6 erhöht wird. Die Formel lautet wie folgt:
E =(O + 4*M + P) / 6
wobei:
E = Erwarteter Zeit- oder Kostenaufwand,
O = Optimistische Schätzung,
M = Wahrscheinlichste Schätzung,
P = Pessimistische Schätzung.
Die Standardabweichung der PERT-Verteilung wird nach folgender Formel berechnet:
Standardabweichung = (P – O) / 6
Für die Schätzung eines gesamten Pfades (analogkritische Pfadmethode) wird ein ähnliches Konzept angewandt, jedoch mit einer kombinierten Standardabweichung aller Aktivitäten.
Beispiel für eine Drei-Punkte-Schätzung und PERT
Ein Team von Fachleuten schätzt die Zeit, die für die Durchführung einer Aktivität benötigt wird. In diesem Beispiel wird die Dauer einer Aktivität mit Hilfe der Drei-Punkte-Schätztechnik geschätzt.Sie kommen auf die folgenden Zahlen:
| Optimistische Schätzung | 15 Tage |
| Pessimistische Schätzung | 24 Tage |
| Wahrscheinlichste Schätzung | 30 Tage |
Die Werte reichen von 15 Tagen (optimistisch)bis 30 Tagen (pessimistisch). Eine Dauer von 24 Tagen wird als die wahrscheinlichste Zeit angesehen, die für die Fertigstellung der Arbeiten benötigt wird.
Berechnung der erwarteten Dauer mit einer Dreiecksverteilung
Die erwartete Dauer mit einer Dreiecksverteilung wird wie folgt berechnet:
Endgültige Schätzung = (15 + 30 + 24) / 3.
Die endgültige Schätzung nach dieser Methode beträgt 23, was im Grunde der ungewichtete Durchschnitt der drei Schätzungen ist.
Berechnung der erwarteten Dauer mit der PERT-Beta-Verteilung
Die erwartete Dauer kann auch mit der PERT-Methode berechnet werden:
Endgültige Schätzung (Erwartungswert) = (15 + 4×24 + 30) / 6.
Der sich daraus ergebende Erwartungswert beträgt 23,5 Tage und ist damit größer als die endgültige Schätzung nach der Dreiecksmethode. Dies ist auf die höhere Gewichtung (d.h. den Multiplikator von 4) zurückzuführen, die der „wahrscheinlichsten“ Schätzung zugewiesen wird.
Die Standardabweichung dieser Schätzung ist:
Standardabweichung = (30 – 15) / 6 = 2,5
Bestimmung der Wahrscheinlichkeiten der erwarteten Dauer
Nach der Berechnung der erwarteten Dauer und der Standardabweichung kann der Projektleiter die Wahrscheinlichkeiten (ca.):
| Bereich | Wahrscheinlichkeit | Untergrenze | Obergrenze |
| 1 x Standardabweichung | 68.3% | 21 | 26 |
| 2 x Standardabweichung | 95.5% | 18,5 | 28,5 |
| 3 x Standardabweichung | 99.7% | 16 | 31 |
Mit einer Wahrscheinlichkeit von 68,3% wird die Dauer der Tätigkeit zwischen 21 und 26 Tagen liegen. Bei einer Spanne von 18,5 bis 28,5 Tagen liegt die Wahrscheinlichkeit bei 95,5 %. Die Verwendung von 3 Standardabweichungen deckt fast die Gesamtheit aller Datenpunkte ab und ergibt eine Wahrscheinlichkeit von 99,7 %, dass die Dauer letztendlich zwischen 16 und 31 Tagen liegen wird.
Zusammenfassung
Die endgültige Schätzung nach der Dreiecksmethode betrug 23, verglichen mit 23,5 nach der PERT-Methode. Dies liegt daran, dass bei der Dreiecksmethode der „wahrscheinlichste“ Fall höher gewichtet wird, der in unserem Fall nicht genau dem Mittelwert (oder ungewichteten Durchschnitt) der optimistischen und der pessimistischen Schätzung entspricht.
Bei der PERT-Methode können die Wahrscheinlichkeiten der Wertebereiche berücksichtigt werden. Dies ist dann sinnvoll, wenn die Qualität der Schätzungen schwankt, z.B. wenn die Differenz zwischen optimistischer und pessimistischer Schätzung bei verschiedenen Aktivitäten stark abweicht. In diesem Fall spiegelt die Verwendung von Bandbreiten und deren Wahrscheinlichkeiten die Streuung und das Vertrauensniveau der zugrundeliegenden Schätzungen wider.
Schlussfolgerung
Die Schätzung von Aktivitäten im Hinblick auf ihren Zeit- und Kostenbedarf ist für die Planung und Terminierung von Projekten und Aktivitäten von entscheidender Bedeutung. Bei vielen Projekten sind genauere Schätzungen, wie z.B. parametrische Schätzungen, die auf statistischen Korrelationen vergleichbarer Projekte in der Vergangenheit basieren, nicht verfügbar. Die Drei-Punkte-Schätztechnik bietet einen guten Ansatz, um in solchen Situationen Top-Down- oder Expertenschätzungen zu verarbeiten und auszugleichen.
Die PERT-Verteilung ist wahrscheinlich die genaueste Methode, um diese schlechtesten, besten und wahrscheinlichsten Fälle zu einer einzigen Zahl (Erwartungswert) oder einem Wertebereich zusammenzufassen. Dank der Verwendung der Standardabweichung berücksichtigt sie sowohl die inhärenten Unsicherheiten als auch die mögliche Streuung der Schätzungen.
Das mag der Grund dafür sein, dass PERT immer noch eine gängige Methode für die Projektschätzung und -planung ist, obwohl es schon seit einigen Jahrzehnten existiert und schon von unseren Großeltern verwendet worden sein könnte (wenn sie Projektmanager gewesen wären).
