Ein digitaler Magnitudenkomparator ist eine kombinierte Schaltung, die zwei digitale oder binäre Zahlen vergleicht, um herauszufinden, ob eine binäre Zahl gleich, kleiner oder größer als die andere binäre Zahl ist. Wir entwerfen logischerweise eine Schaltung, die zwei Eingänge hat, einen für A und einen für B, und drei Ausgänge hat, einen für A > B, einen für A = B und einen für A < B.
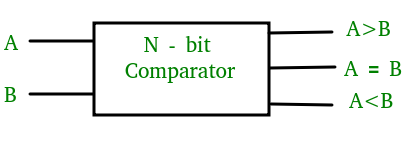
1-Bit-Komparator –
Ein Komparator, der zum Vergleich von zwei Bits dient, wird als Ein-Bit-Komparator bezeichnet. Er besteht aus zwei Eingängen für je zwei Ein-Bit-Zahlen und drei Ausgängen, um zwischen zwei Binärzahlen kleiner, gleich und größer als zu erzeugen.
Die Wahrheitstabelle für einen 1-Bit-Vergleicher ist unten angegeben:
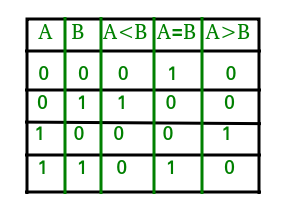
Aus der obigen Wahrheitstabelle können logische Ausdrücke für jeden Ausgang wie folgt ausgedrückt werden:
A>B: AB'A<B: A'BA=B: A'B' + AB
Aus den obigen Ausdrücken können wir die folgende Formel ableiten:

Mit Hilfe dieser booleschen Ausdrücke können wir eine logische Schaltung für diesen Komparator wie folgt realisieren:
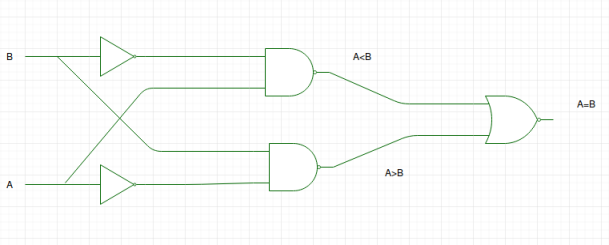
Logisches Diagramm ist falsch
2-Bit-Höhenkomparator –
Ein Komparator, der zum Vergleich von zwei Binärzahlen mit jeweils zwei Bits verwendet wird, wird 2-Bit-Höhenkomparator genannt. Er besteht aus vier Eingängen und drei Ausgängen, um zwischen zwei Binärzahlen kleiner als, gleich und größer als zu erzeugen.
Die Wahrheitstabelle für einen 2-Bit-Vergleicher ist unten angegeben:
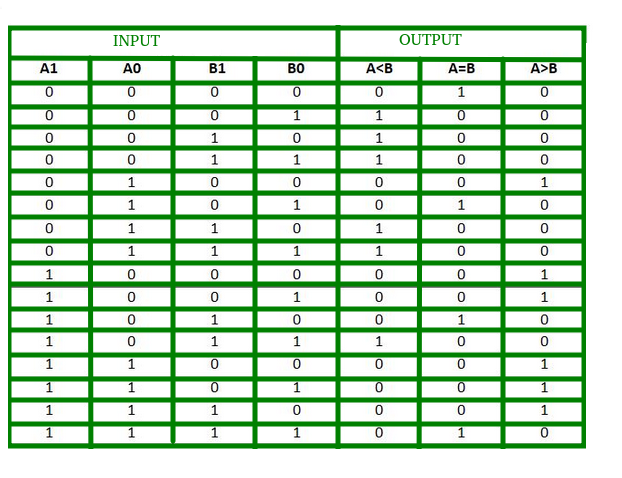
Aus der obigen Wahrheitstabelle kann die K-Map für jeden Ausgang wie folgt gezeichnet werden:



Aus den obigen K-Maps können die logischen Ausdrücke für jeden Ausgang wie folgt ausgedrückt werden:
A>B:A1B1' + A0B1'B0' + A1A0B0'A=B: A1'A0'B1'B0' + A1'A0B1'B0 + A1A0B1B0 + A1A0'B1B0' : A1'B1' (A0'B0' + A0B0) + A1B1 (A0B0 + A0'B0') : (A0B0 + A0'B0') (A1B1 + A1'B1') : (A0 Ex-Nor B0) (A1 Ex-Nor B1)A<B:A1'B1 + A0'B1B0 + A1'A0'B0
Mit Hilfe dieser booleschen Ausdrücke können wir eine logische Schaltung für diesen Komparator wie unten angegeben implementieren:
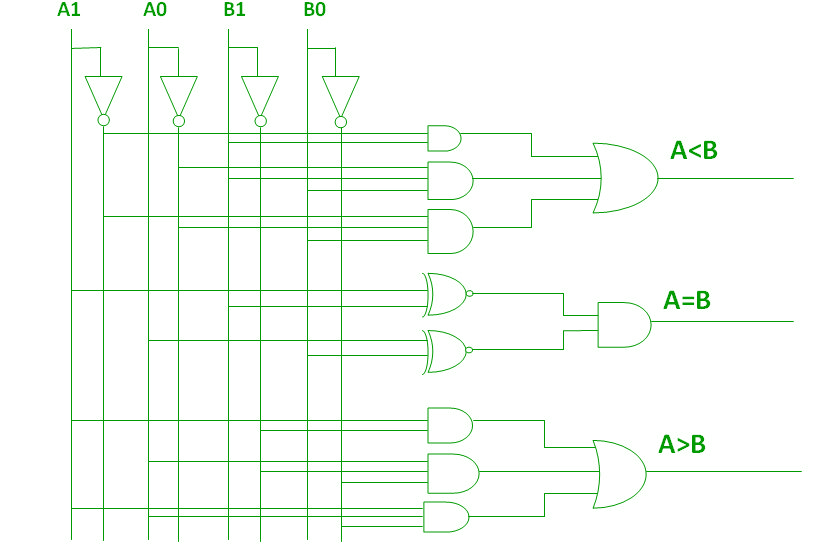
4-Bit-Magnitudenkomparator –
Ein Komparator, der zum Vergleich von zwei Binärzahlen mit jeweils vier Bits verwendet wird, wird 4-Bit-Magnitudenkomparator genannt. Er besteht aus acht Eingängen für je zwei Vier-Bit-Zahlen und drei Ausgängen, um zwischen zwei Binärzahlen kleiner, gleich und größer als zu erzeugen.
In einem 4-Bit-Komparator kann die Bedingung A>B in den folgenden vier Fällen möglich sein:
- Wenn A3 = 1 und B3 = 0
- Wenn A3 = B3 und A2 = 1 und B2 = 0
- Wenn A3 = B3, A2 = B2 und A1 = 1 und B1 = 0
- Wenn A3 = B3, A2 = B2, A1 = B1 und A0 = 1 und B0 = 0
Gleichermaßen kann die Bedingung für A<B in den folgenden vier Fällen möglich sein:
- Wenn A3 = 0 und B3 = 1
- Wenn A3 = B3 und A2 = 0 und B2 = 1
- Wenn A3 = B3, A2 = B2 und A1 = 0 und B1 = 1
- Wenn A3 = B3, A2 = B2, A1 = B1 und A0 = 0 und B0 = 1
Die Bedingung A=B ist nur möglich, wenn alle einzelnen Bits einer Zahl genau mit den entsprechenden Bits einer anderen Zahl übereinstimmen.
Aus den obigen Aussagen lassen sich logische Ausdrücke für jeden Ausgang wie folgt formulieren:
AA, 831331 r: (A3 EioNor 33)A2132′ a (A3 Ex-Nor 133) (A2 Ex-Nor 132)A131′ a (A3 Ex-Nor 33) (A2 ENor132) (Al Ex-Nor 31)A01301
,13: A3’03 a (A3 Ex-Nor 33)A211:12 a (A3 Ex-Nor 83) (A2 Ex-Nor 132)Ar131 a (A3 Ex-Nor 33) (A2 Ex-Nor32) (Al Ex-Nor 131)A0N30
A=B: (A3 Ex-Nor B3) (A2 Ex-Nor 82) (Al Ex-Nor BI) (AO Ex-Nor BO)
Mit Hilfe dieser booleschen Ausdrücke können wir eine logische Schaltung für diesen Komparator wie unten angegeben realisieren:
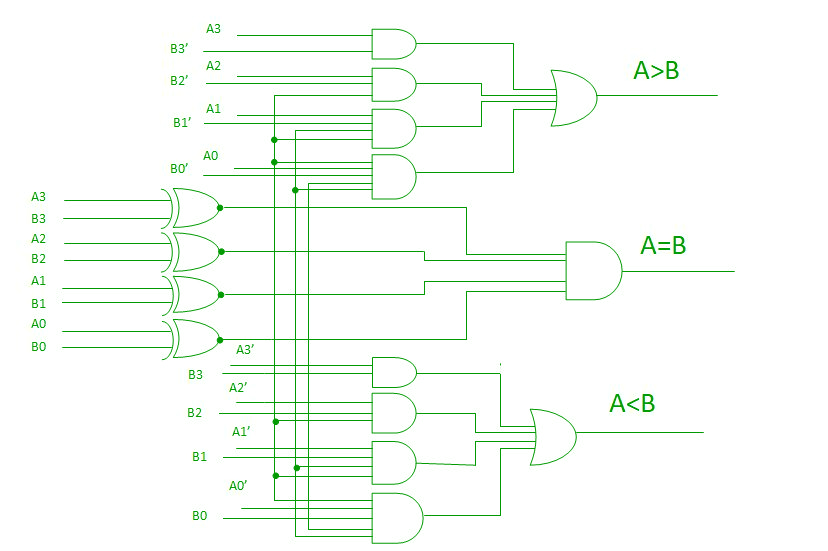
Kaskadenkomparator –
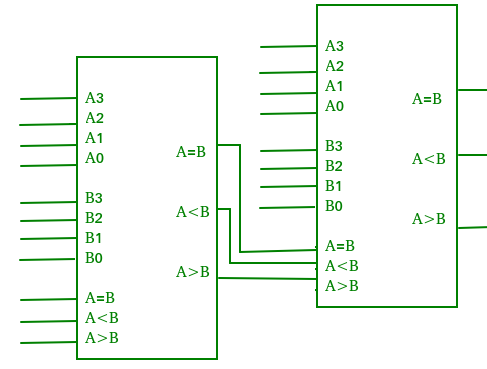
Ein Komparator, der die Vergleichsoperation für mehr als vier Bits durch Kaskadierung von zwei oder mehr 4-Bit-Komparatoren durchführt, wird Kaskadenkomparator genannt. Wenn zwei Komparatoren kaskadiert werden sollen, werden die Ausgänge des Komparators niedrigerer Ordnung mit den entsprechenden Eingängen des Komparators höherer Ordnung verbunden.
Anwendungen von Komparatoren –
- Komparatoren werden in Zentraleinheiten (CPUs) und Mikrocontrollern (MCUs) eingesetzt.
- Sie werden in Steuerungsanwendungen verwendet, in denen die Binärzahlen, die physikalische Variablen wie Temperatur, Position usw. darstellen, mit einem Referenzwert verglichen werden. mit einem Referenzwert verglichen werden.
- Komparatoren werden auch als Prozesssteuerungen und für die Steuerung von Servomotoren verwendet.
- Bei der Passwortverifizierung und bei biometrischen Anwendungen eingesetzt.
