Gepostet am 29. November 2018 von Maximilian Siebert
Heterogenität ist nichts, wovor man sich fürchten muss, sie bedeutet nur, dass es Variabilität in den Daten gibt. Wenn man also verschiedene Studien zusammenführt, um sie zu analysieren oder eine Meta-Analyse durchzuführen, ist es klar, dass man Unterschiede finden wird. Das Gegenteil von Heterogenität ist Homogenität, was bedeutet, dass alle Studien den gleichen Effekt zeigen.
Es ist wichtig zu beachten, dass es verschiedene Arten von Heterogenität gibt:
- Klinisch: Unterschiede bei Teilnehmern, Interventionen oder Ergebnissen
- Methodisch: Unterschiede im Studiendesign, Risiko der Verzerrung
- Statistisch: Variation in den Interventionseffekten oder -ergebnissen
Wir sind an diesen Unterschieden interessiert, weil sie darauf hinweisen können, dass unsere Intervention möglicherweise nicht jedes Mal auf die gleiche Weise funktioniert. Durch die Untersuchung dieser Unterschiede kann man ein viel besseres Verständnis dafür erlangen, welche Faktoren die Intervention beeinflussen und welches Ergebnis man bei der nächsten Anwendung der Intervention erwarten kann.
Obwohl klinische und methodische Heterogenität wichtig sind, wird sich dieser Blog auf statistische Heterogenität konzentrieren.
Wie man Heterogenität identifiziert und misst
Eyeball-Test
In Ihrem Forest Plot sollten Sie auf überlappende Konfidenzintervalle achten und nicht darauf, auf welcher Seite Ihre Effektschätzer liegen. Ob die Ergebnisse auf beiden Seiten der Linie ohne Effekt liegen, hat keinen Einfluss auf Ihre Einschätzung, ob Heterogenität vorliegt, aber es kann Ihre Einschätzung beeinflussen, ob die Heterogenität von Bedeutung ist.
Werfen Sie in diesem Sinne einen Blick auf das nachstehende Diagramm und entscheiden Sie, welches Diagramm homogener ist.
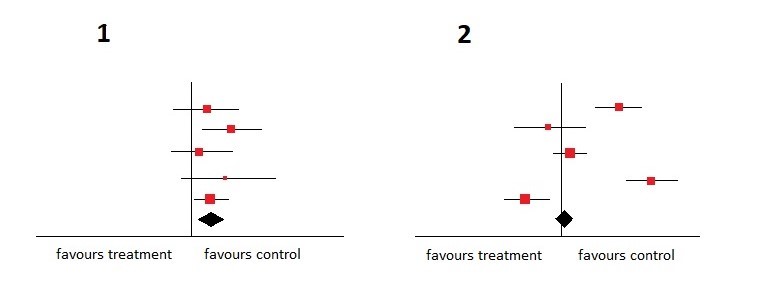
Natürlich ist das homogenere Diagramm das Diagramm Nummer 1. Die Konfidenzintervalle sind alle überlappend und außerdem bevorzugen alle Studien die Kontrollintervention.
Für die Leute, die es lieben, Dinge zu messen, anstatt sie nur mit den Augen zu betrachten, gibt es immer noch einige statistische Methoden, die Ihnen helfen, das Konzept der Heterogenität zu erfassen.
Chi-squared (χ²)-Test
Dieser Test geht von der Nullhypothese aus, dass alle Studien homogen sind, oder dass jede Studie einen identischen Effekt misst, und gibt uns einen p-Wert, um diese Hypothese zu testen. Wenn der p-Wert des Tests niedrig ist, können wir die Hypothese verwerfen und Heterogenität liegt vor.
Da der Test oft nicht empfindlich genug ist und der falsche Ausschluss von Heterogenität schnell passiert, verwenden viele Wissenschaftler einen p-Wert von < 0,1 statt < 0,05 als Grenzwert.
I²
Dieser Test wurde von Professor Julian Higgins entwickelt und misst theoretisch das Ausmaß der Heterogenität, anstatt anzugeben, ob sie vorhanden ist oder nicht.
Schwellenwerte für die Interpretation von I² können irreführend sein, da die Bedeutung der Inkonsistenz von mehreren Faktoren abhängt. Ein grober Leitfaden für die Interpretation lautet wie folgt:
Um die obige Theorie zu verstehen, sehen Sie sich das folgende Beispiel an.
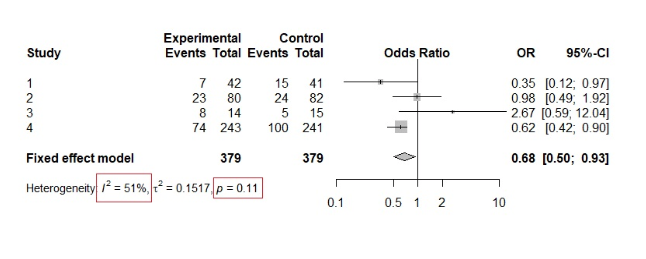
Wir können sehen, dass der p-Wert des Chi-Quadrat-Tests 0,11 beträgt, was die Nullhypothese bestätigt und somit Homogenität nahelegt. Betrachtet man jedoch die Interventionen, so ist bereits eine gewisse Heterogenität in den Ergebnissen zu erkennen. Darüber hinaus beträgt der I²-Wert 51 %, was auf eine mäßige bis erhebliche Heterogenität hindeutet.
Dies ist ein gutes Beispiel dafür, wie der χ²-Test irreführend sein kann, wenn nur wenige Studien in der Meta-Analyse enthalten sind.
Wie geht man mit Heterogenität um?
Wenn Sie die Variabilität in Ihren Ergebnissen erkannt haben, müssen Sie damit umgehen. Hier sind einige Schritte, wie Sie mit diesem Problem umgehen können:
- Prüfen Sie Ihre Daten auf Fehler – Gehen Sie zurück und sehen Sie nach, ob Sie vielleicht etwas falsch eingegeben haben
- Verzichten Sie auf eine Meta-Analyse, wenn die Heterogenität zu groß ist – Nicht jede systematische Übersichtsarbeit braucht eine Meta-Analyse
- Untersuchen Sie die Heterogenität – Dies kann durch Subgruppenanalyse oder Meta-Regression
- Durchführen einer Meta-Analyse mit zufälligen Effekten – Bedenken Sie, dass dieser Ansatz für Heterogenität gilt, die nicht erklärt werden kann, weil sie auf Zufall zurückzuführen ist
- Ändern Sie die Effektmaße – Nehmen wir an, Sie verwenden die Risikodifferenz und haben eine hohe Heterogenität, dann versuchen Sie es mit dem Risikoverhältnis oder der Odds Ratio
(1) Fletcher, J. Was ist Heterogenität und ist sie wichtig? BMJ 2007; 334 :94
(3) https://www.mathsisfun.com/data/chi-square-test.html
