Vor einigen Jahren schrieb Scott Fortmann-Roe einen großartigen Aufsatz mit dem Titel „Understanding the Bias-Variance Tradeoff“
Während sich die Datenwissenschaft zu einem anerkannten Beruf mit eigenen Tools, Verfahren, Arbeitsabläufen usw. entwickelt, scheint der Fokus oft weniger auf statistischen Prozessen zu liegen, sondern eher auf den spannenderen Aspekten (siehe hier und hier für ein paar Diskussionsbeispiele).
Konzeptuelle Definitionen
Während dies als Überblick über Scotts Aufsatz dient, den Sie für weitere Details und mathematische Einsichten lesen können, beginnen wir mit Fortmann-Roes wörtlichen Definitionen, die für den Beitrag von zentraler Bedeutung sind:
Fehler aufgrund von Verzerrungen: Der Fehler aufgrund von Verzerrungen wird als Differenz zwischen der erwarteten (oder durchschnittlichen) Vorhersage unseres Modells und dem richtigen Wert, den wir vorherzusagen versuchen, betrachtet. Natürlich haben Sie nur ein Modell, so dass es etwas seltsam erscheinen mag, von erwarteten oder durchschnittlichen Vorhersagewerten zu sprechen. Stellen Sie sich jedoch vor, Sie könnten den gesamten Prozess der Modellerstellung mehr als einmal wiederholen: Jedes Mal, wenn Sie neue Daten sammeln und eine neue Analyse durchführen, erstellen Sie ein neues Modell. Aufgrund der Zufälligkeit der zugrunde liegenden Datensätze werden die resultierenden Modelle eine Reihe von Vorhersagen aufweisen. Bias misst, wie weit die Vorhersagen dieser Modelle im Allgemeinen vom korrekten Wert abweichen.
Fehler aufgrund von Varianz: Der Fehler aufgrund der Varianz wird als die Variabilität einer Modellvorhersage für einen bestimmten Datenpunkt betrachtet. Wiederum stellen Sie sich vor, dass Sie den gesamten Modellbildungsprozess mehrfach wiederholen können. Die Varianz gibt an, wie stark die Vorhersagen für einen bestimmten Punkt zwischen verschiedenen Realisierungen des Modells variieren.
Im Wesentlichen ist die Verzerrung ein Maß dafür, wie weit die Vorhersagen eines Modells von der Korrektheit entfernt sind, während die Varianz das Ausmaß ist, in dem diese Vorhersagen zwischen den Modelliterationen variieren.
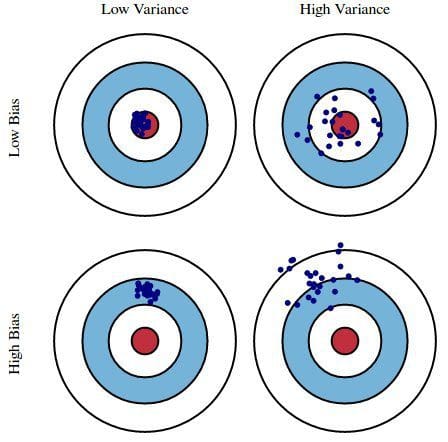
Abb. 1: Grafische Darstellung von Bias und Varianz
Aus Understanding the Bias-Variance Tradeoff, von Scott Fortmann-Roe.
Diskussion
Am Beispiel einer einfachen, fehlerhaften Umfrage zu den Präsidentschaftswahlen werden die Fehler in der Umfrage durch die Zwillingslinse der Verzerrung und der Varianz erklärt: Die Auswahl von Umfrageteilnehmern aus einem Telefonbuch ist eine Quelle der Verzerrung; eine kleine Stichprobengröße ist eine Quelle der Varianz; die Minimierung des gesamten Modellfehlers beruht auf dem Ausgleich der Verzerrungs- und Varianzfehler.
Fortmann-Roe erörtert dann diese Fragen im Zusammenhang mit einem einzigen Algorithmus: k-Nearest Neighbor. Anschließend stellt er einige Schlüsselthemen vor, über die man beim Umgang mit Verzerrungen und Varianz nachdenken sollte, darunter Techniken zur erneuten Stichprobennahme, asymptotische Eigenschaften von Algorithmen und ihre Auswirkungen auf Verzerrungen und Varianzfehler sowie die Bekämpfung der eigenen Annahmen sowohl in Bezug auf die Daten als auch auf deren Modellierung.
Der Aufsatz endet mit der Feststellung, dass diese beiden Konzepte im Kern eng mit Über- und Unteranpassung verbunden sind. Meiner Meinung nach ist dies der wichtigste Punkt:
Wenn mehr und mehr Parameter zu einem Modell hinzugefügt werden, steigt die Komplexität des Modells und die Varianz wird unser Hauptanliegen, während die Verzerrung stetig abnimmt. Je mehr polynomiale Terme beispielsweise zu einer linearen Regression hinzugefügt werden, desto größer wird die Komplexität des resultierenden Modells. Mit anderen Worten, der Bias hat eine negative Ableitung erster Ordnung als Reaktion auf die Modellkomplexität, während die Varianz eine positive Steigung hat.

Abbildung 2: Bias und Varianz tragen zum Gesamtfehler bei
Aus Understanding the Bias-Variance Tradeoff, von Scott Fortmann-Roe.
Fortmann-Roe beendet den Abschnitt über Über- und Unteranpassung, indem er auf einen anderen seiner großartigen Aufsätze (Accurately Measuring Model Prediction Error) verweist und dann zu der sehr zustimmungsfähigen Empfehlung übergeht, dass „auf Wiederholungsstichproben basierende Maße wie die Kreuzvalidierung theoretischen Maßen wie den Aikake’s Information Criteria vorzuziehen sind.“
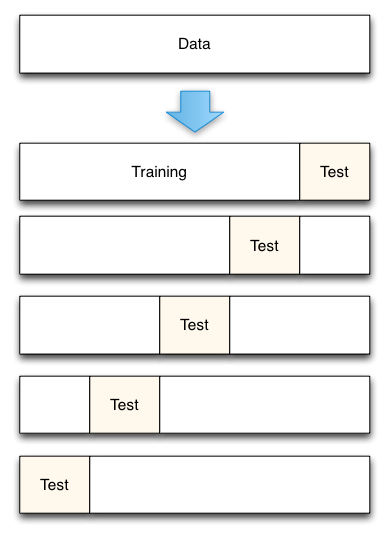
Fig. 3: 5-Fold cross-validation data split
From Accurately Measuring Model Prediction Error, by Scott Fortmann-Roe.
Natürlich ist bei der Kreuzvalidierung die Anzahl der zu verwendenden Faltungen (k-fache Kreuzvalidierung, richtig?), der Wert von k eine wichtige Entscheidung. Je niedriger der Wert ist, desto größer ist die Verzerrung in den Fehlerschätzungen und desto geringer ist die Varianz. Umgekehrt, wenn k gleich der Anzahl der Instanzen gesetzt wird, ist die Verzerrung der Fehlerschätzung sehr gering, aber es besteht die Möglichkeit einer hohen Varianz. Der Kompromiss zwischen Verzerrung und Varianz ist selbst für die routinemäßigsten statistischen Auswertungsmethoden wie die k-fache Kreuzvalidierung wichtig zu verstehen.
Leider scheint auch die Kreuzvalidierung im modernen Zeitalter der Datenwissenschaft bisweilen ihren Reiz verloren zu haben, aber das ist eine Diskussion für ein anderes Mal.
Ich empfehle die Lektüre des gesamten Aufsatzes von Scott Fortmann-Roe über den Kompromiss zwischen Verzerrung und Varianz sowie seinen Beitrag über die Messung von Modellvorhersagefehlern.
Verwandtes:
- Big Data, Bible Codes, and Bonferroni
- Data Science of Variable Selection: Ein Überblick
- Datensätze über Algorithmen
