Link State Routing ist eine Technik, bei der jeder Router das Wissen über seine Nachbarschaft mit jedem anderen Router im Internetnetzwerk teilt.
Die drei Schlüssel zum Verständnis des Link State Routing Algorithmus:
- Wissen über die Nachbarschaft: Anstatt seine Routingtabelle zu senden, sendet ein Router nur die Informationen über seine Nachbarschaft. Ein Router sendet seine Identitäten und Kosten der direkt angeschlossenen Verbindungen an andere Router.
- Flooding: Jeder Router sendet die Informationen an jeden anderen Router im Internetnetzwerk mit Ausnahme seiner Nachbarn. Dieser Vorgang wird als Flooding bezeichnet. Jeder Router, der das Paket empfängt, sendet die Kopien an alle seine Nachbarn. Schließlich erhält jeder Router eine Kopie der gleichen Information.
- Informationsaustausch: Ein Router sendet die Informationen nur dann an jeden anderen Router, wenn sich die Informationen ändern.
Link State Routing hat zwei Phasen:
Reliable Flooding
- Anfangszustand: Jeder Knoten kennt die Kosten seiner Nachbarn.
- Endzustand: Jeder Knoten kennt den gesamten Graphen.
Routenberechnung
Jeder Knoten verwendet Dijkstra’s Algorithmus auf dem Graphen, um die optimalen Routen zu allen Knoten zu berechnen.
- Der Link-State-Routing-Algorithmus ist auch als Dijkstra’s Algorithmus bekannt, der verwendet wird, um den kürzesten Weg von einem Knoten zu jedem anderen Knoten im Netzwerk zu finden.
- Der Dijkstra-Algorithmus ist ein iterativer Algorithmus, der die Eigenschaft hat, dass nach der k-ten Iteration des Algorithmus die Wege mit den geringsten Kosten für k Zielknoten bekannt sind.
Lassen Sie uns einige Notationen beschreiben:
- c( i , j): Verbindungskosten von Knoten i zu Knoten j. Wenn die Knoten i und j nicht direkt verbunden sind, dann ist c(i , j) = ∞.
- D(v): Es definiert die Kosten des Pfades vom Quellknoten zum Zielknoten v, der derzeit die geringsten Kosten hat.
- P(v): Es definiert den vorherigen Knoten (Nachbar von v) zusammen mit dem aktuellen Pfad mit den geringsten Kosten von der Quelle zu v.
- N: Es ist die Gesamtzahl der im Netzwerk verfügbaren Knoten.
Algorithmus
InitializationN = {A} // A is a root node.for all nodes vif v adjacent to Athen D(v) = c(A,v)else D(v) = infinityloopfind w not in N such that D(w) is a minimum.Add w to NUpdate D(v) for all v adjacent to w and not in N:D(v) = min(D(v) , D(w) + c(w,v))Until all nodes in N
In dem obigen Algorithmus folgt auf einen Initialisierungsschritt die Schleife. Die Anzahl der Durchläufe der Schleife ist gleich der Gesamtzahl der im Netz verfügbaren Knoten.
Lassen Sie uns das anhand eines Beispiels nachvollziehen:
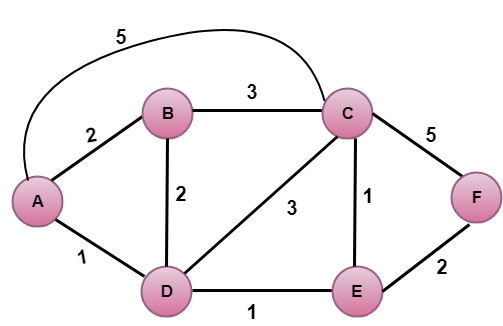
In der obigen Abbildung ist der Ausgangsknoten A.
Schritt 1:
Der erste Schritt ist ein Initialisierungsschritt. Der derzeit bekannte Pfad mit den geringsten Kosten von A zu seinen direkt angeschlossenen Nachbarn B, C und D ist 2, 5 bzw. 1. Die Kosten von A nach B werden auf 2, von A nach D auf 1 und von A nach C auf 5 gesetzt. Die Kosten von A nach E und F werden auf unendlich gesetzt, da sie nicht direkt mit A verbunden sind.
| Schritt | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
Schritt 2:
In der obigen Tabelle sehen wir, dass der Knoten D den Pfad mit den geringsten Kosten in Schritt 1 enthält. Daher wird er in N hinzugefügt. Nun müssen wir einen Pfad mit den geringsten Kosten durch den Scheitelpunkt D bestimmen.
a) Berechnung des kürzesten Pfades von A nach B
b) Berechnung des kürzesten Pfades von A nach C
c) Berechnung des kürzesten Pfades von A nach E
Anmerkung: Der Scheitelpunkt D hat keine direkte Verbindung zum Scheitelpunkt E. Daher ist der Wert von D(F) unendlich.
| Schritt | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
| 2 | AD | 2,A | 4,D | 2,D | ∞ |
Schritt 3:
In der obigen Tabelle sehen wir, dass sowohl E als auch B den Weg mit den geringsten Kosten in Schritt 2 haben. Betrachten wir den Scheitelpunkt E. Jetzt bestimmen wir den kostengünstigsten Weg der übrigen Knoten durch E.
a) Berechnung des kürzesten Weges von A nach B.
b) Berechnung des kürzesten Weges von A nach C.
c) Berechnung des kürzesten Weges von A nach F.
| Schritt | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | |
| 3 | ADE | 2,A | 3,E | 4,E |
Schritt 4:
In der obigen Tabelle sehen wir, dass der Knoten B in Schritt 3 den Weg mit den geringsten Kosten hat. Daher wird er in N hinzugefügt. Jetzt bestimmen wir den Weg der geringsten Kosten der übrigen Knoten durch B.
a) Berechnung des kürzesten Weges von A nach C.
b) Berechnung des kürzesten Weges von A nach F.
| Schritt | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | |
| 3 | ADE | 2,A | 3,E | 4,E | ||
| 4 | ADEB | 3,E | 4,E |
Schritt 5:
In der obigen Tabelle sehen wir, dass der Knoten C in Schritt 4 den Weg mit den geringsten Kosten hat. Daher wird er zu N hinzugefügt. Nun bestimmen wir den kostengünstigsten Weg der übrigen Knoten durch C.
a) Berechnung des kürzesten Weges von A nach F.
| Schritt | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | |
|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | ||
| 3 | ADE | 2,A | 3,E | 4,E | |||
| 4 | ADEB | 3,E | 4,E | ||||
| 5 | ADEBC | 4,E |
Endtabelle:
| Schritt | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | |
|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | ||
| 3 | ADE | 2,A | 3,E | 4,E | |||
| 4 | ADEB | 3,E | 4,E | ||||
| 5 | ADEBC | 4,E | |||||
| 6 | ADEBCF |
Nachteil:
Beim Line-State-Routing entsteht durch das Flooding ein hohes Verkehrsaufkommen. Flooding kann eine Endlosschleife verursachen, dieses Problem kann durch die Verwendung des Time-to-leave-Feldes gelöst werden
