Eine Standardabweichung ist eine Zahl, die uns sagt, wie weit eine Reihe von Zahlen auseinander liegt. Eine Standardabweichung kann von 0 bis unendlich reichen. Eine Standardabweichung von 0 bedeutet, dass eine Liste von Zahlen alle gleich sind – sie liegen überhaupt nicht auseinander.
Standardabweichung – Beispiel
Fünf Bewerber haben im Rahmen einer Bewerbung einen IQ-Test gemacht. Ihre Ergebnisse für die drei IQ-Komponenten sind unten dargestellt.
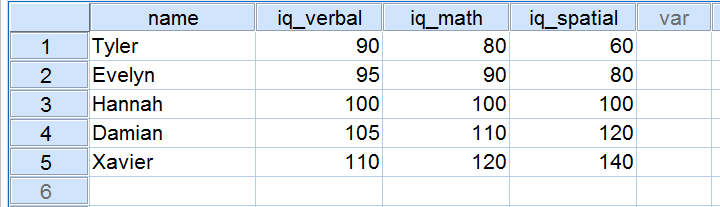
Schauen wir uns nun die Ergebnisse für die drei IQ-Komponenten genau an. Beachten Sie, dass alle drei einen Mittelwert von 100 über unsere 5 Bewerber haben. Allerdings liegen die Werte für iq_verbal näher beieinander als die Werte für iq_math. Außerdem liegen die Werte für iq_spatial weiter auseinander als die Werte für die ersten beiden Komponenten. Das genaue Ausmaß, in dem eine Anzahl von Punkten auseinander liegt, kann als Zahl ausgedrückt werden. Diese Zahl wird als Standardabweichung bezeichnet.
Standardabweichung – Ergebnisse
Im wirklichen Leben inspizieren wir die Rohwerte natürlich nicht visuell, um zu sehen, wie weit sie auseinander liegen. Stattdessen lassen wir sie einfach von einer Software berechnen (dazu später mehr). Die folgende Tabelle zeigt die Standardabweichungen und einige andere Statistiken für unsere IQ-Daten. Beachten Sie, dass die Standardabweichungen das Muster bestätigen, das wir in den Rohdaten gesehen haben.
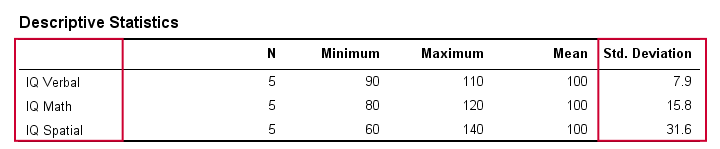
Standardabweichung und Histogramm
Richtig, lassen Sie uns die Dinge ein wenig visueller gestalten. Die folgende Abbildung zeigt die Standardabweichungen und die Histogramme für unsere IQ-Werte. Beachten Sie, dass jeder Balken die Punktzahl eines Bewerbers für eine IQ-Komponente darstellt. Auch hier zeigt sich, dass die Standardabweichungen das Ausmaß angeben, in dem die Werte auseinander liegen.
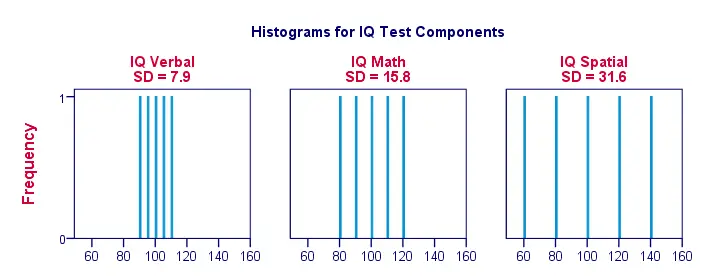
Standardabweichung – Weitere Histogramme
Wenn wir die Daten nur für eine Handvoll Beobachtungen visualisieren, wie in der vorherigen Abbildung, erhalten wir leicht ein klares Bild. Um ein realistischeres Beispiel zu erhalten, werden im Folgenden Histogramme für 1.000 Beobachtungen dargestellt. Wichtig ist, dass diese Histogramme identische Skalen haben; für jedes Histogramm entspricht ein Zentimeter auf der x-Achse etwa 40 „IQ-Komponentenpunkten“.
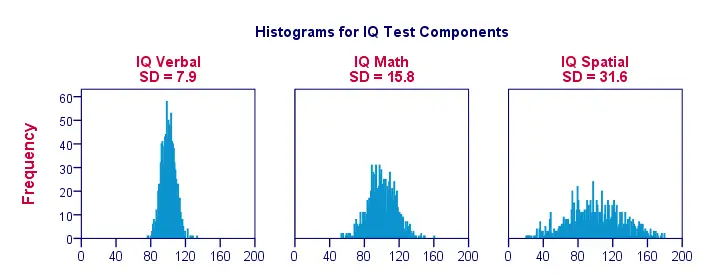
Beachten Sie, dass die Histogramme grobe Schätzungen der Standardabweichungen ermöglichen. Breitere“ Histogramme zeigen größere Standardabweichungen an; die Werte (x-Achse) liegen weiter auseinander. Da alle Histogramme die gleiche Fläche haben (entsprechend 1.000 Beobachtungen), sind höhere Standardabweichungen auch mit ’niedrigeren‘ Histogrammen verbunden.
Standardabweichung – Populationsformel
Wie berechnet Ihre Software nun die Standardabweichungen? Nun, die Grundformel lautet
$$\sigma = \sqrt{\frac{\sum(X – \mu)^2}{N}}$$
wobei
- \(X\) jede einzelne Zahl bezeichnet;
- \(\mu\) bezeichnet den Mittelwert über alle Zahlen und
- \(\sum\) bezeichnet eine Summe.
In Worten: Die Standardabweichung ist die Quadratwurzel aus der durchschnittlichen quadratischen Differenz zwischen jeder einzelnen Zahl und dem Mittelwert dieser Zahlen.
Wichtig ist, dass diese Formel davon ausgeht, dass Ihre Daten die gesamte interessierende Population enthalten (daher „Populationsformel“). Wenn Ihre Daten nur eine Stichprobe aus Ihrer Zielpopulation enthalten, siehe unten.
Populationsformel – Software
Sie können diese Formel in Google Sheets, OpenOffice und Excel verwenden, indem Sie =STDEVP(...) in eine Zelle eingeben. Geben Sie die Zahlen, über die Sie die Standardabweichung ermitteln möchten, zwischen den Klammern an und drücken Sie die Eingabetaste. Die folgende Abbildung veranschaulicht die Idee.
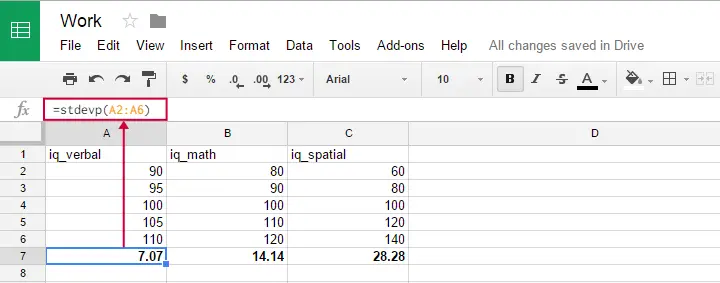
Dummerweise scheint die Formel für die Standardabweichung der Grundgesamtheit in SPSS nicht zu existieren.
Standardabweichung – Stichprobenformel
Nun zu etwas Herausforderndem: Wenn Ihre Daten (annähernd) eine einfache Zufallsstichprobe aus einer (viel) größeren Grundgesamtheit sind, dann wird die vorherige Formel die Standardabweichung in dieser Grundgesamtheit systematisch unterschätzen. Einen unverzerrten Schätzer für die Standardabweichung der Grundgesamtheit erhält man mit
$$S_x = \sqrt{\frac{\sum(X – \overline{X})^2}{N -1}}$
Bezüglich der Berechnungen besteht der große Unterschied zur ersten Formel darin, dass wir durch \(n -1\) statt durch \(n\) teilen. Die Division durch eine kleinere Zahl ergibt ein (etwas) größeres Ergebnis. Dadurch wird die oben erwähnte Unterschätzung genau kompensiert. Für große Stichprobenumfänge haben die beiden Formeln jedoch praktisch identische Ergebnisse.
In GoogleSheets, Open Office und MS Excel verwendet die STDEV-Funktion diese zweite Formel. Es ist auch die (einzige) Standardabweichungsformel, die in SPSS implementiert ist.
Standardabweichung und Varianz
Eine zweite Zahl, die ausdrückt, wie weit ein Satz von Zahlen auseinander liegt, ist die Varianz. Die Varianz ist die quadrierte Standardabweichung. Das bedeutet, dass die Varianz, ähnlich wie die Standardabweichung, sowohl eine Populations- als auch eine Stichprobenformel hat.
Im Prinzip ist es peinlich, dass zwei verschiedene Statistiken im Grunde die gleiche Eigenschaft einer Zahlenmenge ausdrücken. Warum verzichten wir nicht einfach auf die Varianz zugunsten der Standardabweichung (oder umgekehrt)? Die grundsätzliche Antwort ist, dass die Standardabweichung in manchen Situationen wünschenswertere Eigenschaften hat und die Varianz in anderen.
