Siguiente: Importancia de los números adimensionales Subir: Teorema de Pi de Buckingham Anterior: Teorema de Pi de Buckingham
Aplicación del teorema de Pi de Buckingham
El teorema que hemos enunciado es muy general, pero de ninguna manera se limita a la Mecánica de Fluidos. Se utiliza en diversos campos como la Botánica y las Ciencias Sociales y se han escrito libros y volúmenes sobre este tema. Pero no necesitamos mucha teoría para poder aplicarla. Lo que vamos a considerar es un procedimiento para utilizar el teorema y llegar a números adimensionales para un flujo dado.
- Enumerar todas las variables que gobiernan el proceso. Estas variables deben ser independientes entre sí. Por ejemplo, no se debe elegir la densidad, la gravedad y el peso específico. La densidad y el peso específico deberían ser suficientes. Para nuestro problema tenemos F, D, V,
 y
y  . Tenemos n = 5.
. Tenemos n = 5. - Marque las variables repetitivas. En nuestro caso son D, V y
 lo que hace que k = 3 .
lo que hace que k = 3 . - Decide cuántos números adimensionales hay. Para nuestro caso tenemos n – k = 2. Nuestro problema tiene 2 números adimensionales,
 y
y  .
. - Defina los números adimensionales agrupando las variables en n – k grupos de forma que cada grupo tenga todas las variables repetitivas y una variable no repetitiva. Así para nuestro problema tenemos

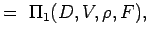

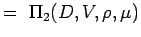
(5.2) Deja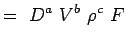

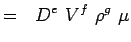
(5.3)
- Expresemos ahora cada variable en términos de sus dimensiones. Utilicemos el sistema MLT según el cual las variables de nuestro problema tienen las siguientes dimensiones.
Variable Dimensiones F, Fuerza M L / T2 o M L T-2 D, Diámetro: L V, Velocidad L/T o LT-1  , Densidad:
, Densidad: M/L3 o ML-3  , Viscosidad
, Viscosidad ML-1T-1 Sustituyendo estas dimensiones en la Ecn. 5.2, tenemos

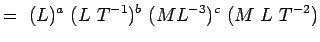

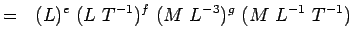
(5.4) O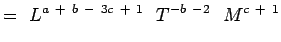

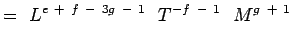
(5.5)
Notando que
 y
y  son adimensionales tenemos,
son adimensionales tenemos,a + b – 3c + 1 = 0; -b – 2 = 0, c + 1 = 0 e + f – 3g – 1 = 0; -f – 1 = 0;g + 1 = 0 (5.6) Resolviendo las ecuaciones se obtiene,
a = -2, b = -2, c = -1 e = -1, f = -1, g = -1 (5.7) Ahora nuestros números adimensionales se convierten en,

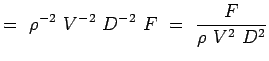

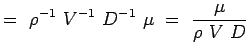
(5.8)
Así hemos encontrado los números adimensionales para el flujo de interés, es decir, el arrastre sobre un cilindro circular. La relación funcional entre los dos números puede expresarse como
Pero nótese que la forma del término ![]() que hemos derivado es algo diferente de lo que suponíamos al principio. El lado derecho de la ecuación es, en realidad, el inverso del número de Reynolds. Esto señala el inconveniente del análisis de que no se puede obtener la forma funcional exacta entre los números
que hemos derivado es algo diferente de lo que suponíamos al principio. El lado derecho de la ecuación es, en realidad, el inverso del número de Reynolds. Esto señala el inconveniente del análisis de que no se puede obtener la forma funcional exacta entre los números ![]() . Cualquier coeficiente o índice obtenido no puede ser determinado por este análisis. Esto debe ser determinado por la experimentación o por los cálculos. Pero como los números son adimensionales podemos escribir,
. Cualquier coeficiente o índice obtenido no puede ser determinado por este análisis. Esto debe ser determinado por la experimentación o por los cálculos. Pero como los números son adimensionales podemos escribir,
Siguiente: Importancia de los números adimensionales Subir: Teorema Pi de Buckingham Anterior: Teorema Pi de Buckingham
(c) Aerospace, Mechanical & Mechatronic Engg. 2005
Universidad de Sidney
