Una desviación estándar es un número que nos indica
hasta qué punto se separa un conjunto de números.Una desviación estándar puede ir de 0 a infinito. Una desviación estándar de 0 significa que una lista de números son todos iguales -no se separan en absoluto.
Desviación estándar – Ejemplo
Cinco solicitantes hicieron un test de CI como parte de una solicitud de empleo. Sus puntuaciones en tres componentes del CI se muestran a continuación.
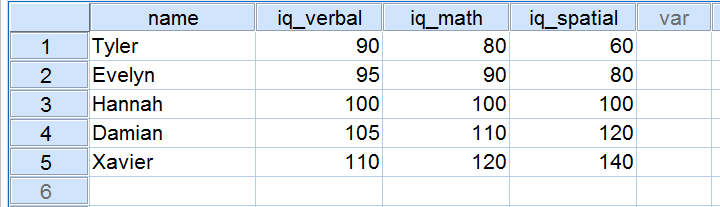
Ahora, observemos detenidamente las puntuaciones de los 3 componentes del CI. Observe que los tres tienen una media de 100 sobre nuestros 5 solicitantes. Sin embargo, las puntuaciones de iq_verbal están más cerca que las de iq_math. Además, las puntuaciones de iq_spatial están más separadas que las de los dos primeros componentes. El grado exacto de separación de las puntuaciones puede expresarse con un número. Este número se conoce como desviación estándar.
Desviación estándar – Resultados
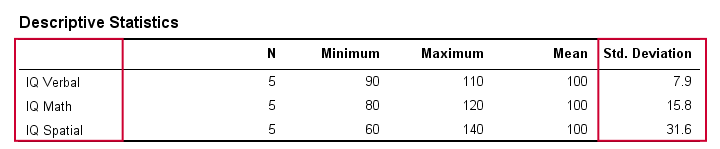
En la vida real, obviamente no inspeccionamos visualmente las puntuaciones brutas para ver la distancia entre ellas. En su lugar, simplemente haremos que un software las calcule por nosotros (más adelante). La siguiente tabla muestra las desviaciones estándar y algunas otras estadísticas de nuestros datos de CI. Observe que las desviaciones estándar confirman el patrón que vimos en los datos brutos.
Desviación estándar e histograma
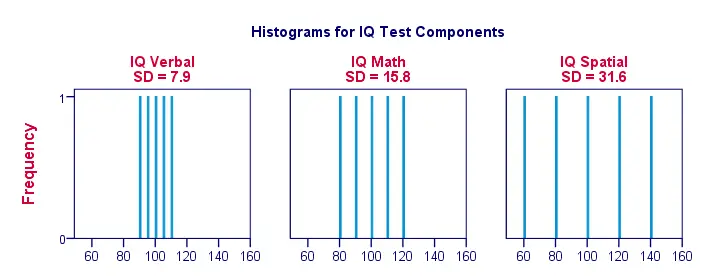
Bien, hagamos las cosas un poco más visuales. La siguiente figura muestra las desviaciones estándar y los histogramas de nuestras puntuaciones de CI. Tenga en cuenta que cada barra representa la puntuación de un solicitante en un componente de CI. Una vez más, vemos que las desviaciones estándar indican el grado de separación de las puntuaciones.
Desviación estándar – Más histogramas
Cuando visualizamos los datos de sólo un puñado de observaciones como en la figura anterior, vemos fácilmente una imagen clara. Para un ejemplo más realista, presentaremos a continuación histogramas para 1.000 observaciones. Es importante destacar que estos histogramas tienen escalas idénticas; para cada histograma, un centímetro en el eje x corresponde a unos 40 «puntos de componente de CI».
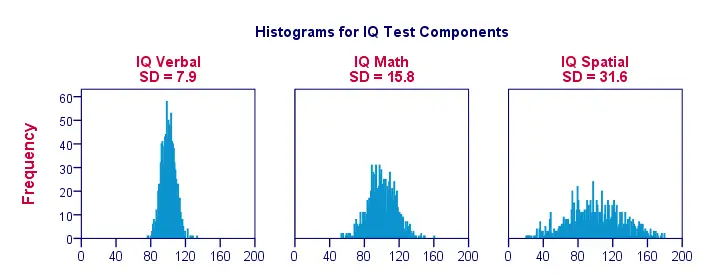
Nótese cómo los histogramas permiten hacer estimaciones aproximadas de las desviaciones estándar. Los histogramas «más anchos» indican desviaciones estándar mayores; las puntuaciones (eje x) están más separadas. Dado que todos los histogramas tienen áreas de superficie idénticas (correspondientes a 1.000 observaciones), las desviaciones estándar más altas también se asocian con histogramas «más bajos».
Desviación estándar – Fórmula de la población
Entonces, ¿cómo calcula su software las desviaciones estándar? Pues bien, la fórmula básica es
$$\sigma = \sqrt{\frac{suma(X – \mu)^2}{N}$
donde
- (X\) denota cada número por separado;
- (\mu\) denota la media sobre todos los números y
- (\sum\) denota una suma.
En palabras, la desviación estándar es la raíz cuadrada de la diferencia media al cuadrado entre cada número individual y la media de estos números.
Importante, esta fórmula asume que sus datos contienen toda la población de interés (de ahí «fórmula poblacional»). Si sus datos contienen sólo una muestra de su población objetivo, vea a continuación.
Fórmula de población – Software
Puede utilizar esta fórmula en las hojas de Google, OpenOffice y Excel escribiendo =STDEVP(...) en una celda. Especifica los números sobre los que quieres la desviación estándar entre los paréntesis y pulsa Enter. La figura siguiente ilustra la idea.
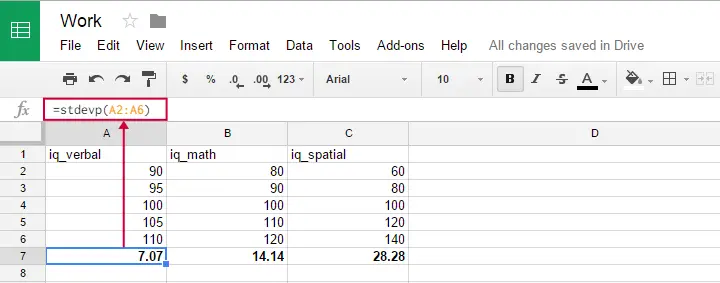
Por desgracia, la fórmula de la desviación estándar de la población no parece existir en SPSS.
Desviación estándar – Fórmula de la muestra
Ahora, algo desafiante: si sus datos son (aproximadamente) una simple muestra aleatoria de alguna población (mucho) mayor, entonces la fórmula anterior subestimará sistemáticamente la desviación estándar en esta población. Un estimador insesgado de la desviación típica de la población se obtiene utilizando
$S_x = \sqrt{\frac{suma(X – \overline{X})^2}{N -1}$
Respecto a los cálculos, la gran diferencia con la primera fórmula es que dividimos por \(n -1\) en lugar de \(n\). Dividiendo por un número menor se obtiene un resultado (ligeramente) mayor. Esto compensa precisamente la mencionada subestimación. Sin embargo, para tamaños de muestra grandes, las dos fórmulas tienen resultados prácticamente idénticos.
En GoogleSheets, Open Office y MS Excel, la función STDEV utiliza esta segunda fórmula. También es la (única) fórmula de desviación estándar implementada en SPSS.
Desviación estándar y varianza
Un segundo número que expresa la distancia entre un conjunto de números es la varianza. La varianza es la desviación estándar al cuadrado. Esto implica que, de forma similar a la desviación estándar, la varianza tiene una fórmula poblacional y otra muestral.
En principio, es incómodo que dos estadísticas diferentes expresen básicamente la misma propiedad de un conjunto de números. ¿Por qué no descartamos la varianza en favor de la desviación estándar (o a la inversa)? La respuesta básica es que la desviación estándar tiene propiedades más deseables en algunas situaciones y la varianza en otras.
