El enrutamiento de estado de enlace es una técnica en la que cada router comparte el conocimiento de su vecindad con todos los demás routers de la red interna.
Las tres claves para entender el algoritmo de enrutamiento de estado de enlace:
- Conocimiento de la vecindad: En lugar de enviar su tabla de enrutamiento, un router envía la información sobre su vecindad solamente. Un router difunde sus identidades y el coste de los enlaces conectados directamente a otros routers.
- Inundación: Cada router envía la información a todos los demás routers de la red interna, excepto a sus vecinos. Este proceso se conoce como Flooding. Cada router que recibe el paquete envía las copias a todos sus vecinos. Finalmente, todos y cada uno de los routers reciben una copia de la misma información.
- Compartir información: Un router envía la información a todos los demás routers sólo cuando se produce el cambio en la información.
El enrutamiento de estado de enlace tiene dos fases:
Inundación fiable
- Estado inicial: Cada nodo conoce el coste de sus vecinos.
- Estado final: Cada nodo conoce todo el grafo.
Cálculo de la ruta
Cada nodo utiliza el algoritmo de Dijkstra en el grafo para calcular las rutas óptimas a todos los nodos.
- El algoritmo de enrutamiento de estado de enlace también se conoce como algoritmo de Dijkstra que se utiliza para encontrar el camino más corto de un nodo a cada uno de los otros nodos de la red.
- El algoritmo de Dijkstra es iterativo, y tiene la propiedad de que después de la kª iteración del algoritmo, los caminos de menor coste son bien conocidos para k nodos de destino.
Describamos algunas notaciones:
- c( i , j): Coste del enlace desde el nodo i al nodo j. Si los nodos i y j no están directamente enlazados, entonces c(i , j) = ∞.
- D(v): Define el coste del camino desde el código fuente al destino v que tiene el menor coste actualmente.
- P(v): Define el nodo anterior (vecino de v) junto con el camino actual de menor coste desde el origen hasta v.
- N: Es el número total de nodos disponibles en la red.
Algoritmo
InitializationN = {A} // A is a root node.for all nodes vif v adjacent to Athen D(v) = c(A,v)else D(v) = infinityloopfind w not in N such that D(w) is a minimum.Add w to NUpdate D(v) for all v adjacent to w and not in N:D(v) = min(D(v) , D(w) + c(w,v))Until all nodes in N
En el algoritmo anterior, un paso de inicialización es seguido por el bucle. El número de veces que se ejecuta el bucle es igual al número total de nodos disponibles en la red.
Entendamos a través de un ejemplo:
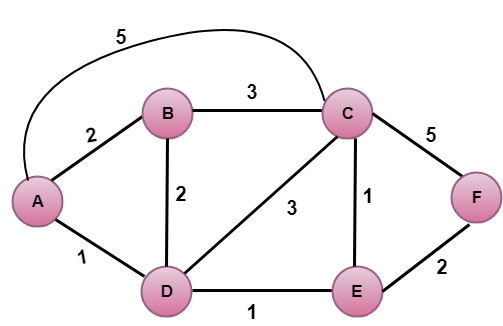
En la figura anterior, el vértice origen es A.
Paso 1:
El primer paso es un paso de inicialización. La ruta de menor coste actualmente conocida desde A a sus vecinos directamente unidos, B, C, D son 2,5,1 respectivamente. El coste de A a B se establece en 2, de A a D se establece en 1 y de A a C se establece en 5. El coste de A a E y F se establece en infinito ya que no están directamente vinculados a A.
| Paso | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
Paso 2:
En la tabla anterior, observamos que el vértice D contiene el camino de menor coste en el paso 1. Por lo tanto, se añade en N. Ahora, necesitamos determinar un camino de menor coste a través del vértice D.
a) Calcular el camino más corto de A a B
b) Calcular el camino más corto de A a C
c) Calcular el camino más corto de A a E
Nota: El vértice D no tiene enlace directo con el vértice E. Por lo tanto, el valor de D(F) es infinito.
| Paso | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
| 2 | AD | 2,A | 4,D | 2,D | ∞ |
Paso 3:
En la tabla anterior, observamos que tanto E como B tienen el camino de menor coste en el paso 2. Consideremos el vértice E. Ahora, determinamos el camino de menor coste de los vértices restantes a través de E.
a) Calcular el camino más corto de A a B.
b) Calcular el camino más corto de A a C.
c) Calcular el camino más corto de A a F.
| Paso | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | |
| 3 | ADE | 2,A | 3,E |
Paso 4:
En la tabla anterior, observamos que el vértice B tiene el camino de menor coste en el paso 3. Por lo tanto, se añade en N. Ahora, determinamos el camino de menor coste de los vértices restantes a través de B.
a) Calcular el camino más corto de A a C.
b) Calcular el camino más corto de A a F.
| Paso | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | |
| 3 | ADE | 2,A | 3,E | |||
| 4 | ADEB | 3,E | 4,E |
Paso 5:
En la tabla anterior, observamos que el vértice C tiene el camino de menor coste en el paso 4. Por lo tanto, se añade en N. Ahora, determinamos el camino de menor coste de los vértices restantes a través de C.
a) Calcular el camino más corto de A a F.
| Paso | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | |
| 3 | ADE | 2,A | 3,E | |||
| 4 | ADEB | |||||
| 5 | ADEBC |
Tabla final:
| Paso | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | |
| 3 | ADE | 2,A | 3,E | |||
| 4 | ADEB | 3,E | 4,E | |||
| 5 | ADEBC | |||||
| 6 | ADEBCF |
Desventaja:
Se crea mucho tráfico en el enrutamiento de estado de línea debido al Flooding. El Flooding puede causar un bucle infinito, este problema puede ser resuelto utilizando el campo Time-to-leave
