La estimación de tiempos, esfuerzos y costes es una de las partes más críticas de la gestión de proyectos. Esto se debe a la importancia fundamental de estas estimaciones para toda la planificación del proyecto y, en particular, para el alcance, el calendario y la línea de base de los costes. Una de las técnicas de estimación sugeridas en el PMI Project Management Body of Knowledge (PMBOK 6ª ed., cap. 6.4, 7.2) es la estimación de tres puntos utilizada con la distribución triangular, Beta o PERT. Presentaremos estos métodos en este artículo.
¿Qué es la técnica de estimación de tres puntos?
La estimación de tres puntos es un enfoque sencillo pero útil para estimar el tiempo o el coste de los elementos de trabajo. Según la metodología del PMI, se utiliza en los grupos de procesos «Estimación de la duración de la actividad» y «Estimación de los costes». La técnica implica tres estimaciones diferentes que suelen obtenerse de expertos en la materia:
- Estimación optimista,
- Estimación pesimista,
- Estimación más probable.
La estimación optimista es la cantidad esperada de trabajo o tiempo necesario para realizar una actividad suponiendo que no se producen impedimentos y que todo va bien. Representa el llamado mejor escenario posible. El punto pesimista se basa en la suposición de que lo contrario fuera cierto: representa el peor escenario. Aunque ambas estimaciones se refieren a los puntos extremos del rango de resultados esperados, se supone que las estimaciones son algo realistas.
El tercer punto refleja el caso más probable, es la estimación de trabajo o tiempo que se considera más realista. Se podría tener la tentación de utilizar simplemente la media entre los puntos optimista y pesimista sin pensarlo dos veces. Sin embargo, esto puede no ser apropiado para muchos casos. En la práctica, normalmente vale la pena determinar adecuadamente esta estimación más probable, de forma análoga a los otros puntos de estimación.
El resultado de la estimación de tres puntos es la llamada distribución triangular de los valores de tiempo o de los importes de los costes, que comprende las tres estimaciones (véase la ilustración siguiente).
¿Qué es el PERT?
PERT son las siglas de Program Evaluation and Review Technique (Técnica de Evaluación y Revisión de Programas) y fue desarrollado como un sistema avanzado de planificación y gestión del calendario de proyectos por la marina estadounidense en la década de 1950 (fuente: Heldman, PMP Study guide, cap. 4).
Otra historia, no demasiado seria, de su origen fue publicada una vez por un autor anónimo en la revista del PMI (Link; fuente: Anónimo (1975). PERT-el engaño del siglo. Project Management Quarterly, 6(3), 22-23).
En los proyectos del estilo del PMI, el PERT se utiliza principalmente como técnica complementaria al método del camino crítico para programar actividades. Sin embargo, también puede aplicarse a las estimaciones independientes de elementos de trabajo y actividades.
La llamada distribución PERT aprovecha los valores determinados con la técnica de estimación de tres puntos. Básicamente puede utilizarse para todos los niveles de planificación, desde las actividades hasta los proyectos completos. Sin embargo, encontrar la granularidad adecuada para una estimación significativa puede requerir cierto pensamiento crítico y conceptual.
El método PERT implica sobreponderar la estimación «más probable». Transforma la estimación de tres puntos en una curva en forma de campana y permite determinar las probabilidades de los rangos de valores esperados.
¿Cuáles son las diferencias entre la distribución triangular y la distribución PERT de las estimaciones de tres puntos?
Mientras que la distribución triangular sólo tiene en cuenta los tres puntos estimados, el método PERT permite convertir la estimación de tres puntos en una curva en forma de campana, con una distribución casi normal.
El siguiente diagrama ilustra las diferencias entre la distribución PERT, la distribución triangular y la presentación de la estimación de tres puntos como si fuera una distribución normal.
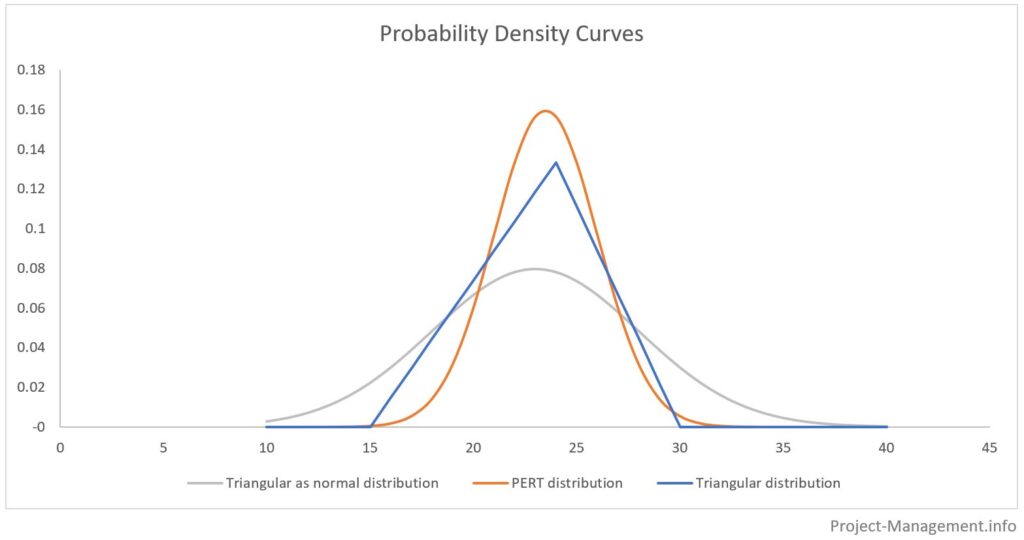
Las áreas bajo las curvas de distribución de probabilidad representan las probabilidades acumuladas de los respectivos rangos de estimaciones. Normalmente, estos rangos se determinan con el valor esperado +/- la desviación estándar multiplicada por 1, 2 y 3. Esto se ilustra en la siguiente figura:
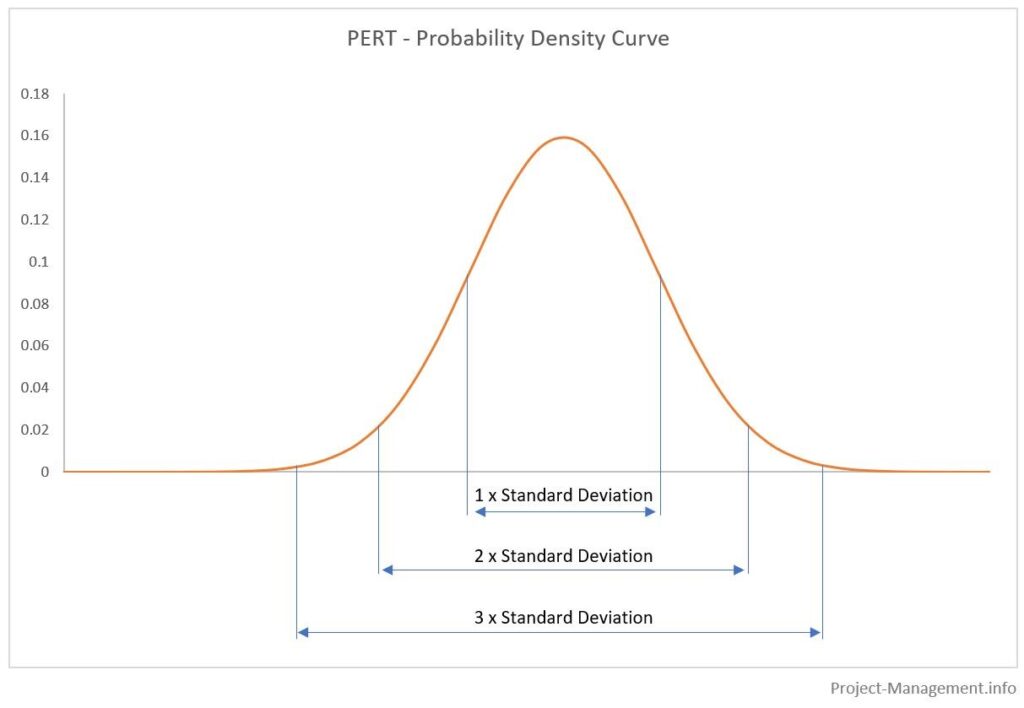
Las probabilidades resultantes (aprox.) son
- 68,3% para 1 desviación estándar,
- 95.5% para 2 desviaciones estándar,
- 99,7% para 3 desviaciones estándar.
Los conocimientos necesarios para el examen PMP se limitan a calcular las estimaciones esperadas y a conocer las diferentes probabilidades (fuente). Por lo tanto, no cubriremos los detalles estadísticos y los antecedentes en este artículo – usted puede encontrar esos detalles en Riskamp.
Use esta calculadora para determinar las estimaciones de tres puntos y el PERT.
¿Cómo se calcula la estimación de tres puntos?
La distribución triangular
El cálculo simple pero comúnmente utilizado implica el promedio o la media de los 3 valores estimados. La fórmula de esta distribución triangular es:
E =(O + M + P) / 3
donde:
E = Cantidad esperada de tiempo o coste,
O = Estimación optimista,
M = Estimación más probable,
P = Estimación pesimista.
El PMBOK utiliza t(E), t(O), t(M) y t(P) como variables para las estimaciones de tiempo y c(E), c(O), c(M) y c(P).
El peso de cada estimación en esta ecuación es idéntico. Así, el caso «más probable» no afecta a la estimación final más que las 2 estimaciones menos probables. Esto es diferente del método de distribución beta.
La distribución beta PERT
La distribución beta PERT tiene en cuenta que el caso «más probable» es más probable que ocurra, lo que se refleja en un multiplicador para esa estimación. La metodología del PMI sugiere este cálculo como alternativa a la distribución triangular para las estimaciones de costes (sin embargo, opinamos que también puede utilizarse para las estimaciones de tiempo).
En este método, la estimación más probable recibe un multiplicador de 4 mientras que el divisor global se incrementa a 6. La fórmula es la siguiente:
E =(O + 4*M + P) / 6
donde:
E = Cantidad esperada de tiempo o coste,
O = Estimación optimista,
M = Estimación más probable,
P = Estimación pesimista.
La desviación estándar de la distribución PERT se calcula mediante la fórmula:
Desviación estándar = (P – O) / 6
Para la estimación de una ruta completa (método de la ruta crítica análoga), se aplica un concepto similar pero utilizando una desviación estándar combinada de todas las actividades.
Ejemplo de estimación en tres puntos y PERT
Un equipo de expertos en la materia está estimando el tiempo necesario para completar una actividad. En este ejemplo, la duración de una actividad se estima utilizando la técnica de estimación de tres puntos.Llegan a los siguientes números:
| Estimación optimista | 15 días |
| Estimación pesimista | 24 días |
| Estimación más probable | 30 días |
Los valores van de 15 días (optimista)a 30 días (pesimista). Se considera que una duración de 24 días es la cantidad de tiempo más probable que se necesita para completar el trabajo.
Calcular la duración esperada con una distribución triangular
La duración esperada utilizando una distribución triangular se calcula de la siguiente manera:
Estimación final = (15 + 30 + 24) / 3.
La estimación final resultante con este método es 23, que es básicamente la media no ponderada de las 3 estimaciones.
Calcular la duración esperada utilizando la distribución beta del PERT
La duración esperada también puede calcularse con el método PERT:
Estimación final (valor esperado) = (15 + 4×24 + 30) / 6.
El valor esperado resultante es de 23,5 días, que es mayor que la estimación final determinada con el método triangular. Esto se debe al mayor peso (es decir, el multiplicador de 4) que se asigna a la estimación «más probable».
La desviación estándar de esta estimación es:
Desviación estándar = (30 – 15) / 6 = 2,5
Determinación de las probabilidades de la duración esperada
Haber calculado la duración esperada y la desviación estándar permite al director del proyecto determinar las probabilidades (aprox.):
| Rango | Probabilidad | Límite inferior | Límite superior |
| 1 x desviación estándar | 68.3% | 21 | 26 |
| 2 x desviación estándar | 95.5% | 18,5 | 28,5 |
| 3 x desviación estándar | 99.7% | 16 | 31 |
Con un 68,3% de probabilidad, la duración de la actividad estará entre 21 y 26 días. Para un rango de 18,5 a 28,5 días, la probabilidad es del 95,5%. El uso de 3 desviaciones estándar cubre casi la totalidad de los puntos de datos y determina una probabilidad del 99,7% de que la duración se sitúe finalmente entre 16 y 31 días.
Resumen
La estimación final con el método triangular fue de 23, frente a 23,5 con el método PERT. Esto se debe a que el último asigna una mayor ponderación al caso «más probable» que, en nuestro caso, no es exactamente la media (o promedio no ponderado) de la estimación optimista y pesimista.
El uso del método PERT permite tener en cuenta las probabilidades de los rangos de valores. Esto es útil si la calidad de las estimaciones varía, por ejemplo, si la diferencia entre las estimaciones optimistas y pesimistas se desvía significativamente entre las diferentes actividades. En este caso, el uso de rangos y sus probabilidades reflejará la dispersión y el nivel de confianza de las estimaciones subyacentes.
Conclusión
La estimación de las actividades con respecto a sus requisitos de tiempo y coste es crucial para la planificación y programación de proyectos y actividades. En muchos proyectos, no se dispone de estimaciones más precisas, como las estimaciones paramétricas, basadas en correlaciones estadísticas de proyectos comparables en el pasado, por ejemplo. La técnica de estimación de tres puntos ofrece un buen enfoque para procesar y equilibrar las estimaciones descendentes o de expertos en la materia en tales situaciones.
La distribución PERT es probablemente el método más preciso para agregar estos peores, mejores y más probables casos en una sola cifra (valor esperado) o un rango de valores. Gracias al uso de la desviación estándar, tiene en cuenta tanto las incertidumbres inherentes como la posible dispersión de las estimaciones.
Esta podría ser la razón por la que el PERT sigue siendo un método común en la estimación y programación de proyectos, a pesar de que ha existido durante algunas décadas y ya podría haber sido utilizado por nuestros abuelos (si hubieran sido gestores de proyectos).
