Hace unos años, Scott Fortmann-Roe escribió un gran ensayo titulado «La comprensión de la compensación de sesgo-varianza.»
Como la ciencia de datos se transforma en una profesión aceptada con su propio conjunto de herramientas, procedimientos, flujos de trabajo, etc., a menudo parece haber menos de un enfoque en los procesos estadísticos en favor de los aspectos más emocionantes (ver aquí y aquí para un par de discusiones de ejemplo).
Definiciones conceptuales
Aunque esto servirá como una visión general del ensayo de Scott, que se puede leer para obtener más detalles y conocimientos matemáticos, comenzaremos con las definiciones literales de Fortmann-Roe que son fundamentales para la pieza:
Error por sesgo: El error por sesgo se toma como la diferencia entre la predicción esperada (o promedio) de nuestro modelo y el valor correcto que estamos tratando de predecir. Por supuesto, sólo tiene un modelo, por lo que hablar de valores de predicción esperados o medios puede parecer un poco extraño. Sin embargo, imagine que puede repetir todo el proceso de construcción del modelo más de una vez: cada vez que recoja nuevos datos y ejecute un nuevo análisis creando un nuevo modelo. Debido a la aleatoriedad de los conjuntos de datos subyacentes, los modelos resultantes tendrán un rango de predicciones. El sesgo mide lo lejos que están en general las predicciones de estos modelos del valor correcto.
Error debido a la varianza: El error debido a la varianza se toma como la variabilidad de la predicción de un modelo para un punto de datos determinado. De nuevo, imagine que puede repetir todo el proceso de construcción del modelo varias veces. La varianza es cuánto varían las predicciones para un punto dado entre diferentes realizaciones del modelo.
Esencialmente, el sesgo es lo alejadas que están las predicciones de un modelo de la corrección, mientras que la varianza es el grado en que estas predicciones varían entre las iteraciones del modelo.
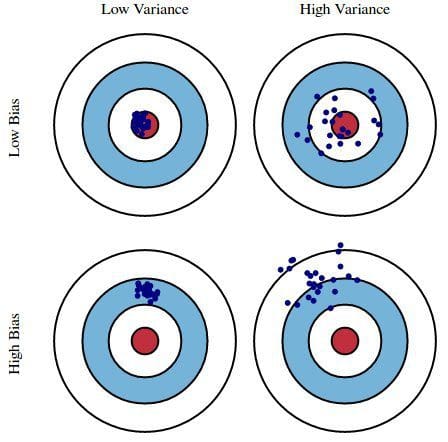
Figura 1: Ilustración gráfica del sesgo y la varianza
De Understanding the Bias-Variance Tradeoff, por Scott Fortmann-Roe.
Discusión
Usando una simple encuesta defectuosa sobre las elecciones presidenciales como ejemplo, los errores en la encuesta se explican a través de las lentes gemelas del sesgo y la varianza: la selección de los participantes en la encuesta a partir de una guía telefónica es una fuente de sesgo; un tamaño de muestra pequeño es una fuente de varianza; la minimización del error total del modelo se basa en el equilibrio de los errores de sesgo y varianza.
Fortmann-Roe pasa a discutir estas cuestiones en relación con un único algoritmo: k-Nearest Neighbor. A continuación, proporciona algunas cuestiones clave en las que pensar a la hora de gestionar el sesgo y la varianza, incluidas las técnicas de remuestreo, las propiedades asintóticas de los algoritmos y su efecto en los errores de sesgo y varianza, y la lucha contra los propios supuestos en relación con los datos y su modelización.
El ensayo termina afirmando que, en su esencia, estos dos conceptos están estrechamente relacionados con el sobreajuste y el infraajuste. En mi opinión, éste es el punto más importante:
A medida que se añaden más y más parámetros a un modelo, la complejidad del mismo aumenta y la varianza se convierte en nuestra principal preocupación, mientras que el sesgo disminuye constantemente. Por ejemplo, cuanto más términos polinómicos se añadan a una regresión lineal, mayor será la complejidad del modelo resultante. En otras palabras, el sesgo tiene una derivada de primer orden negativa en respuesta a la complejidad del modelo, mientras que la varianza tiene una pendiente positiva.

Fig. 2: Contribución del sesgo y la varianza al error total
De Understanding the Bias-Variance Tradeoff, por Scott Fortmann-Roe.
Fortmann-Roe termina la sección sobre el sobreajuste y el infraajuste señalando otro de sus magníficos ensayos (Accurately Measuring Model Prediction Error), y pasando después a la recomendación, muy acertada, de que «las medidas basadas en el remuestreo, como la validación cruzada, deben preferirse a las medidas teóricas, como el criterio de información de Aikake.»
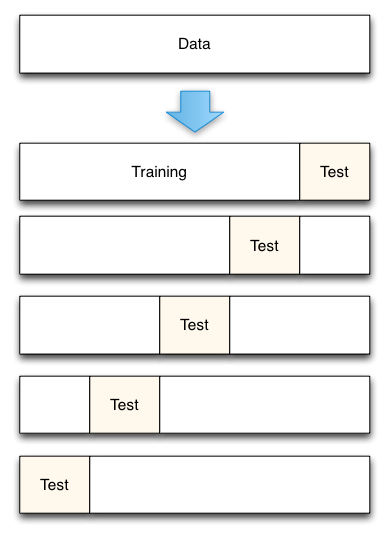
Fig. 3: División de datos de validación cruzada de 5 veces
De Accurately Measuring Model Prediction Error, por Scott Fortmann-Roe.
Por supuesto, con la validación cruzada, el número de pliegues a utilizar (k-validación cruzada, ¿verdad?), el valor de k es una decisión importante. Cuanto menor sea el valor, mayor será el sesgo en las estimaciones de error y menor será la varianza. Por el contrario, cuando k se establece igual al número de instancias, la estimación del error tiene un sesgo muy bajo pero tiene la posibilidad de una varianza alta. La compensación entre sesgo y varianza es claramente importante para entender incluso el más rutinario de los métodos de evaluación estadística, como la validación cruzada k-fold.
Desgraciadamente, la validación cruzada también parece, a veces, haber perdido su encanto en la era moderna de la ciencia de los datos, pero esa es una discusión para otro momento.
Recomiendo la lectura del ensayo completo de Scott Fortmann-Roe sobre el equilibrio entre el sesgo y la varianza, así como su artículo sobre la medición del error de predicción del modelo.
Relación:
- Grandes datos, códigos bíblicos y Bonferroni
- Ciencia de datos de selección de variables: A Review
- Datasets Over Algorithms
