A esto se le llama a veces la teoría de las mareas «estáticas», una teoría que surgió por primera vez en los famosos Principia de Isaac Newton. Una vez identificadas las fuerzas que producen las mareas, Newton, y otros que le siguieron, concibieron un hipotético océano global en equilibrio estático con estas fuerzas, un equilibrio que requería un esferoide aprolado de agua que cubriera la tierra. «Prolongado» significa que la esfera en cuestión se ha estirado a lo largo de una línea que une dos polos; no los polos geográficos en este caso, sino los polos en línea con el cuerpo celeste (la luna o el sol) que provoca la deformación de la hipotética esfera oceánica. Si volvemos a mirar el gráfico que ilustra las fuerzas de tracción en el módulo anterior, podemos imaginar fácilmente que el agua converge en estos polos para producir dos «protuberancias de marea», términos que siguen siendo muy populares en los libros de texto actuales.
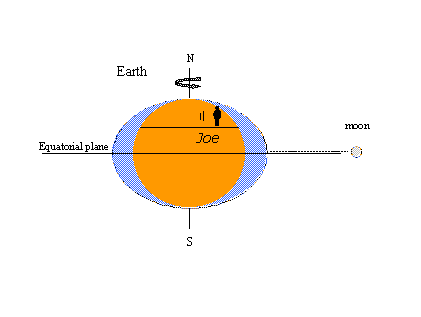
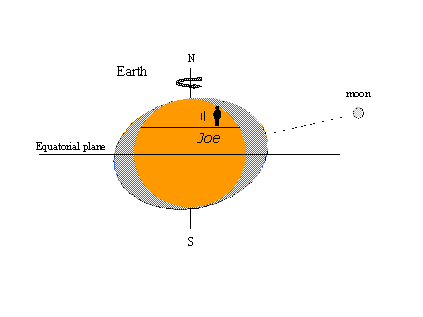
La razón de la popularidad de la teoría del equilibrio -el concepto de las protuberancias de marea, al menos- es que es fácil explicar ciertos fenómenos de marea bien conocidos con imágenes. En la imagen de la izquierda, un observador imaginario llamado Joe gira con la Tierra y se encuentra con las protuberancias estáticas en forma de mareas altas. Cuando la luna cruza el meridiano opuesto en el otro lado de la tierra, la marea alta se repite doce horas después. En un día lunar que dura 24 horas y 50 minutos en tiempo de reloj (solar) se producen dos pleas y dos bajadas. En la figura de la derecha, la Luna ha avanzado en su órbita alrededor de la Tierra hasta situarse al norte del ecuador (declinación norte). Las protuberancias estáticas se mueven para mantenerse en línea con la luna y ahora Joe se encuentra con una desigualdad diurna en las mareas altas (mareas altas sucesivas de altura desigual). La máxima declinación lunar, al norte o al sur del ecuador, produce mareas tropicales; las mareas que ocurren cuando la luna está en el ecuador se llaman mareas ecuatoriales.Las mareas tropicales-ecuatoriales se repiten dos veces en un intervalo de 27 1/3 días – el mes trópico cubre un ciclo completo en la declinación lunar. Todas estas observaciones son consistentes con la teoría del equilibrio.
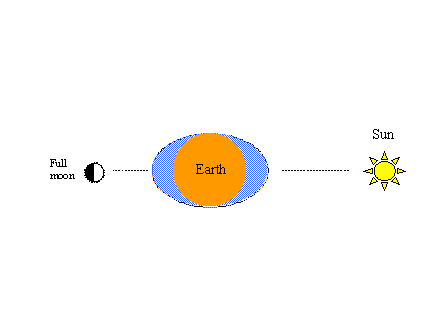
Otro fenómeno que es fácil de demostrar de esta manera es el conocido ciclo de primavera-piña. La gravedad solar también produce un par de protuberancias marinas en el hipotético océano. Cuando las fuerzas de tracción del sol y de la luna están alineadas, se producen mareas vivas de mayor alcance (máximas más altas y mínimas más bajas), como se muestra en la figura de la izquierda. Al igual que en las figuras anteriores, cuando la luna complete otro medio ciclo en su órbita -esta vez de luna llena a luna nueva- se producirán de nuevo mareas de primavera.
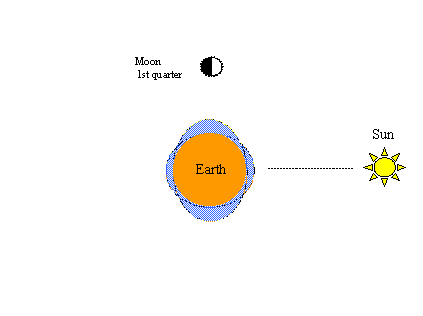
La figura de abajo a la derecha ilustra la porción neap del ciclo primavera-noche; es decir, cuando la luna está en el primer cuarto (o el tercer cuarto) de ese ciclo, las fuerzas de tracción lunar y solar están completamente desalineadas, tendiendo a contrarrestarse mutuamente, y se producen mareas neap de menor alcance (máximos más bajos y mínimos más altos). Dos ciclos de primavera-pernocta (dos primaveras y dos puestas) se completan en 29 ½ días, el mismo período de tiempo requerido para que la luna complete una órbita completa de la tierra con respecto al sol.
Otros aspectos de la marea observada de acuerdo con la teoría del equilibrio incluyen el ciclo perigeo-apogeo. Este se deriva del hecho de que la órbita de la luna alrededor de la tierra describe una elipse en lugar de un círculo. Las mareas perigeas de mayor alcance se producen en el perigeo lunar, cuando la luna está más cerca de la tierra, y las mareas apogeas de menor alcance se producen en el apogeo lunar, cuando la luna está más lejos de la tierra en su órbita elíptica. El ciclo perigeo-apogeo tarda unos 27 ½ días en completarse.
Aunque la teoría del equilibrio hace un excelente trabajo al explicar los fenómenos cíclicos de las mareas y los periodos de recurrencia asociados a muchos de ellos, es un ejemplo de un modelo de comportamiento ideal -algo que funciona para el propósito previsto aunque no se adhiera a la verdad en todas las circunstancias. No tenemos que buscar mucho esos casos. La Tierra sólo está parcialmente cubierta por sus aguas, las masas de tierra impiden que cualquier cosa que se parezca a una marea se desplace completamente a su alrededor, y las observaciones de las mareas reales demuestran que no responden instantáneamente a las fuerzas productoras de mareas de la luna y el sol como exige la teoría.
