Introducción :
La similitud del coseno se utiliza para determinar la similitud entre documentos o vectores. Matemáticamente, mide el coseno del ángulo entre dos vectores proyectados en un espacio multidimensional.Hay otras técnicas de medición de la similitud como la distancia euclidiana o la distancia Manhattan disponibles, pero nos centraremos aquí en la similitud del coseno y la distancia del coseno.
La relación entre la similitud del coseno y la distancia del coseno se puede definir como sigue.
- La similitud disminuye cuando la distancia entre dos vectores aumenta

2. La similitud aumenta cuando la distancia entre dos vectores disminuye.

Similaridad del coseno y distancia del coseno:
La similitud del coseno dice que para encontrar la similitud entre dos puntos o vectores necesitamos encontrar el Ángulo entre ellos.
La fórmula para encontrar la similitud del coseno y la distancia es la siguiente:


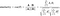
Aquí A=Punto P1,B=Punto P2 (en nuestro ejemplo)
Veamos los distintos valores de Cos Θ para entender la similitud del coseno y la distancia del coseno entre dos puntos de datos(vectores) P1 & P2 considerando dos ejes X e Y.
La siguiente imagen tiene allí casos.
Caso 1: Cuando el ángulo entre los puntos P1 & P2 es de 45 grados entonces
coseno_similitud= Cos 45 = 0.525
Caso 2: Cuando dos puntos P1 & P2 están alejados entre sí y el ángulo entre los puntos es de 90 Grados entonces
coseno_similitud= Cos 90 = 0
Caso 3: Cuando dos puntos P1 & P2 están muy cerca y se encuentra en el mismo eje entre sí y el ángulo entre los puntos es 0 Grado entonces
cosine_similarity= Cos 0 = 1

Bajo la imagen que tiene los siguientes tres casos.
Caso 4: Cuando los puntos P1 & P2 se encuentra frente a dos entre sí y y el ángulo entre los puntos es 180 Grado entonces
cosine_similaridad= Cos 180 = -1
Caso 5: Cuando el ángulo entre los puntos P1 & P2 es 270 Grado entonces
cosine_similaridad= Cos 270 = 0
Caso 6: Cuando el ángulo entre los puntos P1 & P2 es de 360 Grados entonces
coseno_similitud= Cos 360 = 1

Pasemos estos valores de cada uno de los ángulos comentados anteriormente y veamos la Distancia Coseno entre dos puntos.
1 – Coseno_Similar=Coseno_Distancia
Caso 1: Cuando Cos 45 Grados
Sustituyamos los valores en la fórmula anterior.
1-0.525= Coseno_Distancia
0.475 =Coseno_Distancia
Caso 2: Cuando Cos 90 Grado
1-0= Coseno_Distancia
1 =Coseno_Distancia
Caso 3: Cuando Cos 0 Grado
1-1= Coseno_Distancia
0 =Coseno_Distancia
Caso 4: Cuando Cos 180 Grado
1-(-1)= Coseno_Distancia
2 =Coseno_Distancia
Caso 5: Cuando Cos 270 Grado
1-0= Coseno_Distancia
1 =Coseno_Distancia
Caso 6: Cuando Cos 360 Grados
1-1= Coseno_Distancia
0 =Coseno_Distancia
Podemos ver claramente que cuando la distancia es menor la similitud es mayor (los puntos están cerca el uno del otro) y la distancia es mayor ,dos puntos son disímiles (lejos el uno del otro)
La Similitud del Coseno y la Distancia del Coseno es muy utilizada en los sistemas de recomendación para recomendar productos a los usuarios basados en sus gustos.
Algunos ejemplos en los que se utiliza son sitios web como Amazon, Flipkart para recomendar artículos a los clientes para una experiencia personalizada, clasificación y recomendación de películas, etc.
Conclusión : Espero que por ahora tengas una clara comprensión de las matemáticas detrás del cálculo de la similitud del coseno y la distancia del coseno y su uso.
Espero que te guste mi artículo.Por favor, pulsa Clap 👏(50 veces) para motivarme a escribir más.
Quieres conectarte :
Linked In : https://www.linkedin.com/in/anjani-kumar-9b969a39/
Si te gustan mis posts aquí en Medium y deseas que siga haciendo este trabajo, considera apoyarme en patreon
