A Buckingham Pi-tétel alkalmazása

Következő: Előző: Buckingham Pi-tétel

A Buckingham Pi-tétel alkalmazása

A felállított tétel nagyon általános, de semmiképpen sem korlátozódik a folyadékmechanikára. Változatos területeken, például a botanikában és a társadalomtudományokban is alkalmazzák, és könyveket és köteteket írtak erről a témáról. De nincs szükségünk sok elméletre ahhoz, hogy alkalmazni tudjuk. Amit mi megvizsgálunk, az egy olyan eljárás, amellyel a tételt használhatjuk, és egy adott áramláshoz dimenziótlan számokhoz juthatunk.

1. Listázzuk az összes változót, amely a folyamatot irányítja. Ezeknek a változóknak egymástól függetlennek kell lenniük. Például nem szabad kiválasztani a sűrűséget, a gravitációt és a fajsúlyt. A sűrűségnek és a fajsúlynak elegendőnek kell lennie. A mi problémánkhoz F, D, V, és van. Van n = 5.
2. Kijelöljük az ismétlődő változókat. Esetünkben ezek D, V és , így k = 3 .
3. Döntsük el, hogy hány dimenziótlan szám van. A mi esetünkben n – k = 2. A mi feladatunkban 2 nemdimenziós szám van, és .
4. Meghatározzuk a nemdimenziós számokat úgy, hogy a változókat n – k csoportokba csoportosítjuk úgy, hogy minden csoportban az összes ismétlődő változó és egy nem ismétlődő változó legyen. Így a problémánkhoz

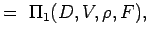
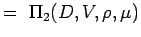
   		(5.2)
   Let
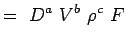
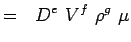
   		(5.3)

5. Most fejezzük ki az egyes változókat a dimenzióik szempontjából. Használjuk az MLT rendszert, amely szerint a problémáink változói a következő dimenziókkal rendelkeznek.
   

   Változó	Dimenziók
   F, erő	M L / T2 vagy M L T-2
   D, átmérő:	L
   V, Sebesség	L/T vagy LT-1
   , Sűrűség:	M/L3 vagy ML-3
   , Viszkozitás	ML-1T-1

   Ezeket a dimenziókat beillesztve az egyenletbe. 5.2-be, megkapjuk

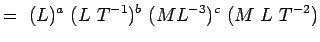
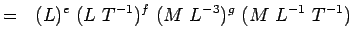
   		(5.4)
   Or
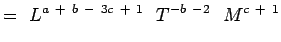
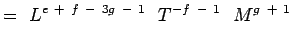
   		(5.5)

   Megállapítva, hogy és nem dimenziósak, van,

   a + b – 3c + 1 = 0; -b – 2 = 0, c + 1 = 0
   e + f – 3g – 1 = 0; -f – 1 = 0;g + 1 = 0	(5.6)

   Az egyenletek feloldásával megkapjuk,

   a = -2, b = -2, c = -1
   e = -1, f = -1, g = -1	(5.7)

   Most a nemdimenziós számaink,

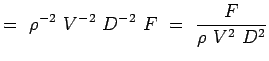
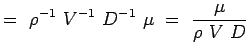
   		(5.8)

Így megtaláltuk a nemdimenziós számokat az érdekes áramlásra, nevezetesen a körhenger körüli légellenállásra. A két szám közötti funkcionális kapcsolat a következőképpen fejezhető ki:

De vegyük észre, hogy az általunk levezetett kifejezés formája némileg eltér attól, amit az elején feltételeztünk. Az egyenlet jobb oldala valójában a Reynolds-szám inverze!Ez rámutat az elemzés hátrányára, hogy a számok közötti pontosfunkcionális formát nem kaphatjuk meg. Bármilyen kapott együtthatót vagy mutatót nem lehet meghatározni ezzel az analízissel. Ezt kísérletekkel vagy számításokkal kell meghatározni. De mivel a számok nem dimenziósak, így nyugodtan írhatjuk,

Next: Előző: Buckingham Pi-tétel

(c) Aerospace, Mechanical & Mechatronic Engg. 2005
Sydney-i Egyetem