Néhány évvel ezelőtt Scott Fortmann-Roe írt egy nagyszerű esszét “A torzítás-variáció tradeoff megértése” címmel.
Ahogy az adattudomány elfogadott szakmává válik, saját eszközkészlettel, eljárásokkal, munkafolyamatokkal stb, gyakran úgy tűnik, hogy kevésbé összpontosítanak a statisztikai folyamatokra az izgalmasabb szempontok javára (lásd itt és itt egy pár példát a vitákról).
Fogalmi definíciók
Míg ez Scott esszéjének áttekintésére szolgál, amelyet további részletekért és matematikai betekintésért elolvashat, kezdjük Fortmann-Roe szó szerinti definícióival, amelyek központi szerepet játszanak a műben:
Error due to Bias: A torzítás miatti hibát a modellünk várható (vagy átlagos) előrejelzése és a helyes érték közötti különbségnek tekintjük, amelyet megpróbálunk megjósolni. Természetesen csak egy modellel rendelkezünk, így a várható vagy átlagos előrejelzési értékekről való beszéd kissé furcsának tűnhet. Képzeljük el azonban, hogy az egész modellépítési folyamatot többször is megismételhetjük: minden alkalommal, amikor új adatokat gyűjtünk, és új elemzést futtatunk, új modellt létrehozva. Az alapul szolgáló adathalmazok véletlenszerűsége miatt az így kapott modellek előrejelzési tartományt fognak tartalmazni. A torzítás azt méri, hogy ezek a modellek előrejelzései általánosságban mennyire térnek el a helyes értéktől.
A variancia miatti hiba: A variancia miatti hiba a modell előrejelzésének egy adott adatpontra vonatkozó varianciáját jelenti. Ismét képzeljük el, hogy a teljes modellépítési folyamatot többször is megismételhetjük. A variancia az, hogy egy adott pontra vonatkozó előrejelzések mennyire változnak a modell különböző megvalósításai között.
Lényegében a torzítás az, hogy a modell előrejelzései mennyire távolodnak el a helyességtől, míg a variancia az, hogy ezek az előrejelzések milyen mértékben változnak a modell iterációi között.
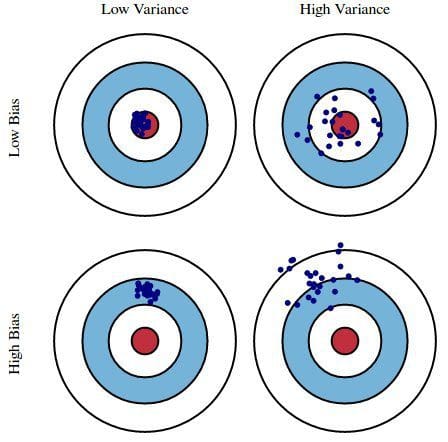
1. ábra: Az előfeszítés és a variancia grafikus szemléltetése
A Scott Fortmann-Roe által írt Understanding the Bias-Variance Tradeoff című könyvből.
Diszkusszió
Egy egyszerű, hibás elnökválasztási felmérést használva példaként, a felmérés hibáit a torzítás és a variancia kettős szemszögéből magyarázzuk: a felmérésben résztvevők telefonkönyvből történő kiválasztása a torzítás forrása; a kis mintanagyság a variancia forrása; a teljes modellhiba minimalizálása a torzítás és a variancia hibáinak kiegyensúlyozásán alapul.
Fortmann-Roe ezután ezeket a kérdéseket egyetlen algoritmusra, a k-Nearest Neighborra vonatkoztatva tárgyalja. Ezután ismertet néhány kulcsfontosságú kérdést, amelyeken el kell gondolkodni a torzítás és a variancia kezelése során, beleértve az újramintázási technikákat, az algoritmusok aszimptotikus tulajdonságait és azok hatását a torzítási és varianciahibákra, valamint az adatokkal és a modellezéssel kapcsolatos feltevésekkel való küzdelmet.
A dolgozat végén azt állítja, hogy e két fogalom alapvetően szorosan kapcsolódik a túl- és alulillesztéshez. Véleményem szerint itt a legfontosabb pont:
Amint egyre több és több paramétert adunk hozzá egy modellhez, a modell bonyolultsága növekszik, és a variancia válik az elsődleges gondunkká, miközben a torzítás folyamatosan csökken. Például minél több polinomiális kifejezést adunk hozzá egy lineáris regresszióhoz, annál nagyobb lesz az eredményül kapott modell komplexitása. Más szóval, a torzításnak negatív elsőrendű deriváltja van a modell összetettségének függvényében, míg a variancia pozitív meredekségű.

2. ábra: A torzítás és a variancia hozzájárulása a teljes hibához
A Scott Fortmann-Roe által írt Understanding the Bias-Variance Tradeoff című könyvből.
Fortmann-Roe a túl- és alulillesztésről szóló részt azzal zárja, hogy rámutat egy másik nagyszerű esszéjére (Accurately Measuring Model Prediction Error), majd rátér arra a rendkívül egyetértő ajánlásra, hogy “az újramintázáson alapuló méréseket, például a kereszt-validálást előnyben kell részesíteni az olyan elméleti mérésekkel szemben, mint az Aikake’s Information Criteria”.
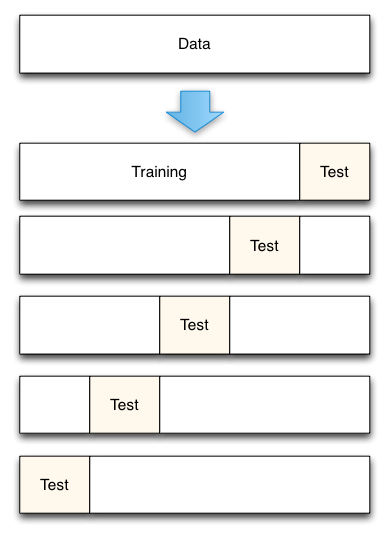
3. ábra: 5-szörös kereszt-validációs adatfelosztás
A Accurately Measuring Model Prediction Error című könyvből, írta Scott Fortmann-Roe.
A kereszthitelesítésnél természetesen fontos döntés, hogy hányszoros (k-szoros kereszthitelesítés, ugye?), k értékét használjuk. Minél kisebb az érték, annál nagyobb a torzítás a hiba becslésekben és annál kisebb a szórás. Ezzel szemben, ha a k értéke megegyezik az esetek számával, akkor a hiba becslése ekkor nagyon alacsony torzítású, de nagy szórás lehetősége van. A torzítás-variáció kompromisszumot nyilvánvalóan fontos megérteni még a legrutinosabb statisztikai kiértékelési módszerek, például a k-szoros kereszt-validálás esetében is.
A kereszt-validálás sajnos időnként úgy tűnik, hogy az adattudomány modern korában elvesztette vonzerejét, de ez egy másik alkalommal tárgyalandó kérdés.
Elolvasásra ajánlom Scott Fortmann-Roe teljes bias-variance tradeoff esszéjét, valamint a modell előrejelzési hibájának méréséről szóló írását.
Kapcsolódó:
- Big Data, Bible Codes, and Bonferroni
- Data Science of Variable Selection: A Review
- Datasets Over Algorithms
