Bevezetés :
A koszinusz hasonlóságot a dokumentumok vagy vektorok közötti hasonlóság meghatározására használják. Matematikailag a többdimenziós térbe vetített két vektor közötti szög koszinuszát méri.léteznek más hasonlóságmérési technikák is, mint például az euklideszi távolság vagy a Manhattan távolság, de mi itt a koszinusz hasonlóságra és a koszinusz távolságra fogunk koncentrálni.
A koszinusz hasonlóság és a koszinusz távolság közötti kapcsolat az alábbiak szerint definiálható.
- A hasonlóság csökken, ha két vektor közötti távolság nő

2. A hasonlóság nő, ha két vektor közötti távolság csökken.

Kozinusz hasonlóság és koszinusz távolság:
A kozinusz hasonlóság azt mondja, hogy két pont vagy vektor hasonlóságának megállapításához meg kell találnunk a köztük lévő szöget.
A koszinusz hasonlóság és a távolság megtalálásának képlete az alábbi:


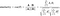
Itt A=P1 pont,B=P2 pont (példánkban)
Lássuk a Cos Θ különböző értékeit, hogy megértsük a koszinusz hasonlóságot és a koszinusz távolságot két adatpont (vektor) P1 & P2 között, figyelembe véve a két X és Y tengelyt.
Az alábbi képen vannak esetek.
1. eset: Ha a P1 & P2 pontok közötti szög 45 fok, akkor
kozinusz-hasonlóság= Cos 45 = 0.525
2. eset: Ha két pont P1 & P2 távol van egymástól és a pontok közötti szög 90 fok, akkor
kozinusz_hasonlóság= Cos 90 = 0
3. eset: Ha két pont P1 & P2 nagyon közel van egymáshoz és ugyanazon a tengelyen fekszik, és a pontok közötti szög 0 fok, akkor
kozin_hasonlóság= Cos 0 = 1

A következő három esetet tartalmazó kép.
4. eset: Ha a P1 & P2 pontok egymással szemben fekszenek és a pontok közötti szög 180 fok, akkor
kozin_hasonlóság= Cos 180 = -1
5. eset: Ha a P1 & P2 pontok közötti szög 270 fok, akkor
kozin_hasonlóság= Cos 270 = 0
6. eset: Ha a P1 & P2 pontok közötti szög 360 fok, akkor
cosine_similarity= Cos 360 = 1

Adjuk át az egyes szögek fent tárgyalt értékeit, és nézzük meg a két pont közötti koszinusz távolságot.
1 – KoszinuszHasonlóság=KozinuszTávolság
1. eset: Ha Cos 45 fok
Helyettesítsük a fenti képletben szereplő értékeket .
1-0.525= Cosine_Distance
0.475 =Kozinusztávolság
2. eset: Amikor Cos 90 fok
1-0= Kozinusztávolság
1 =Kozinusztávolság
3. eset: Amikor Cos 0 fok
1-1= Kozinusztávolság
0 =Kozinusztávolság
4. eset: Amikor Cos 180 fok
1-(-1)= Cosine_Distance
2 =Cosine_Distance
5. eset: Amikor Cos 270 fok
1-0= Cosine_Distance
1 =Cosine_Distance
6. eset: Ha Cos 360 fok
1-1= Cosine_Distance
0 =Cosine_Distance
Tisztán láthatjuk, hogy ha a távolság kisebb, akkor a hasonlóság nagyobb (a pontok közel vannak egymáshoz) és a távolság nagyobb ,két pont nem hasonló (távol vannak egymástól)
A Cosine Similarity és Cosine Distance erősen használatos az ajánlórendszerekben, hogy termékeket ajánljanak a felhasználóknak az általuk kedvelt és nem kedvelt termékek alapján.
Néhány példa, ahol ezt használják, olyan weboldalak, mint az Amazon, Flipkart, hogy termékeket ajánljanak az ügyfeleknek a személyre szabott élmény érdekében, filmek értékelése és ajánlása stb.
Következtetés : Remélem, mostanra már világosan megértetted a koszinusz hasonlóság és a koszinusz távolság kiszámítása mögött álló matematikát és annak használatát.
Remélem, tetszett a cikkem.Kérlek, nyomj tapsot 👏(50-szer), hogy motiválj, hogy tovább írjak.
Kapcsolódni szeretnék :
Linked In : https://www.linkedin.com/in/anjani-kumar-9b969a39/
Ha tetszenek a bejegyzéseim itt a Mediumon, és szeretnéd, hogy folytassam ezt a munkát, fontold meg, hogy támogass a patreonon
.
