A Link State Routing egy olyan technika, amelyben minden útválasztó megosztja a szomszédságára vonatkozó ismereteket az internethálózat minden más útválasztójával.
A Link State Routing algoritmus megértésének három kulcsa:
- A szomszédság ismerete: Az útválasztótábla küldése helyett az útválasztó csak a szomszédságára vonatkozó információkat küldi. Egy útválasztó a közvetlenül kapcsolódó linkek identitását és költségét sugározza a többi útválasztónak.
- Flooding: Minden útválasztó elküldi az információt az internethálózat minden más útválasztójának, kivéve a szomszédait. Ezt a folyamatot Floodingnak nevezzük. Minden útválasztó, amelyik megkapja a csomagot, elküldi a másolatokat az összes szomszédjának. Végül minden egyes útválasztó megkapja ugyanannak az információnak a másolatát.
- Információmegosztás: Egy útválasztó csak akkor küldi el az információt minden más útválasztónak, ha az információban változás következik be.
A Link State Routing két fázisból áll:
Reliable Flooding
- Kezdeti állapot: Minden csomópont ismeri a szomszédai költségeit.
- Végső állapot: Minden csomópont ismeri a teljes gráfot.
Útvonalszámítás
Minden csomópont a Dijkstra algoritmust használja a gráfon az összes csomóponthoz vezető optimális útvonal kiszámításához.
- A Link state routing algoritmus Dijkstra algoritmus néven is ismert, amely arra szolgál, hogy megtalálja a legrövidebb utat egy csomópontból a hálózat minden más csomópontjához.
- A Dijkstra algoritmus iteratív, és rendelkezik azzal a tulajdonsággal, hogy az algoritmus k-adik iterációja után a legkisebb költségű utak jól ismertek k célcsomóponthoz.
Írd le néhány jelölést:
- c( i , j): Ha i és j csomópontok nem közvetlenül kapcsolódnak egymáshoz, akkor c(i , j) = ∞.
- D(v): Meghatározza annak az útvonalnak a költségét a forráskódtól a v célállomásig, amelynek jelenleg a legkisebb a költsége.
- P(v): Meghatározza az előző csomópontot (v szomszédját) a forrásból v-be vezető aktuálisan legkisebb költségű úttal együtt.
- N: A hálózatban rendelkezésre álló összes csomópont száma.
Algoritmus
InitializationN = {A} // A is a root node.for all nodes vif v adjacent to Athen D(v) = c(A,v)else D(v) = infinityloopfind w not in N such that D(w) is a minimum.Add w to NUpdate D(v) for all v adjacent to w and not in N:D(v) = min(D(v) , D(w) + c(w,v))Until all nodes in N
A fenti algoritmusban egy inicializálási lépés után következik a ciklus. A ciklus végrehajtásának száma megegyezik a hálózatban rendelkezésre álló csomópontok teljes számával.
Egy példán keresztül értsük meg:
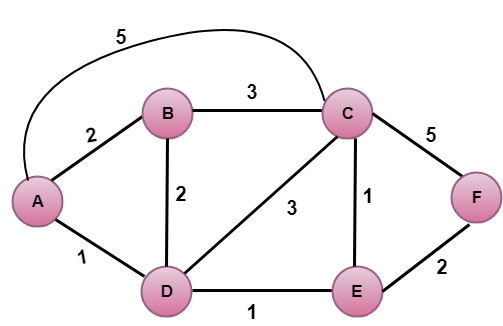
A fenti ábrán a forráscsomópont A.
1. lépés:
Az első lépés egy inicializálási lépés. A jelenleg ismert legkisebb költségű útvonal A-tól a közvetlenül kapcsolódó szomszédaihoz, B, C, D-hez 2,5,1, illetve. Az A és B közötti költséget 2-re, az A és D közötti költséget 1-re, az A és C közötti költséget pedig 5-re állítjuk. Az A és E és F közötti költséget végtelenre állítjuk, mivel ezek nem kapcsolódnak közvetlenül A-hoz.
| Szint | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
2. lépés:
A fenti táblázatban megfigyelhetjük, hogy a D csúcs tartalmazza a legkisebb költségű utat az 1. lépésben. Ezért hozzáadjuk az N-hez. Most meg kell határoznunk egy legkisebb költségű utat a D csúcson keresztül.
a) A legrövidebb út kiszámítása A-tól B-ig
b) A legrövidebb út kiszámítása A-tól C-ig
c) A legrövidebb út kiszámítása A-tól E-ig
Megjegyzés: A D csúcsnak nincs közvetlen kapcsolata az E csúcshoz, ezért a D(F) értéke végtelen.
| Step | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
| 2 | AD | 2,A | 4,D | 2,D | ∞ |
3. lépés:
A fenti táblázatban megfigyelhetjük, hogy mind E, mind B a 2. lépésben a legkisebb költségű útvonallal rendelkezik. Tekintsük az E csúcsot. Most határozzuk meg a többi csúcs legkisebb költségű útját E-n keresztül.
a) A legrövidebb út kiszámítása A-tól B-ig.
b) A legrövidebb út kiszámítása A-tól C-ig.
c) A legrövidebb út kiszámítása A-tól F-ig.
| Step | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | |
|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | ||
| 3 | ADE | 2,A | 3,E | 4,E |
4. lépés:
A fenti táblázatban megfigyelhetjük, hogy a 3. lépésben a B csúcsnak van a legkisebb költségű útvonala. Ezért hozzáadjuk az N-hez. Most meghatározzuk a többi csúcs legkisebb költségű útját B-n keresztül.
a) A legrövidebb út kiszámítása A-tól C-ig.
b) A legrövidebb út kiszámítása A-tól F-ig.
| Step | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | |
|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | ||
| 3 | AD | 2,A | 3,E | 4,E | |||
| 4 | ADEB | 3,E | 4,E |
5. lépés:
A fenti táblázatban megfigyelhetjük, hogy a 4. lépésben a C csúcsnak van a legkisebb költségű útvonala. Ezért hozzáadjuk az N-hez. Most meghatározzuk a többi csúcs legkisebb költségű útját C-n keresztül.
a) A legrövidebb út kiszámítása A-tól F-ig.
| Step | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | ||
|---|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | ||
| 2 | AD | 2,A | 4,D | 2,D | ∞ | |||
| 3 | ADE | 2,A | 3,E | 4,E | ||||
| 4 | ADEB | 3,E | 4,E | |||||
| 5 | ADEBC | 4,E |
A végső táblázat:
| Step | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | ||
|---|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | ||
| 2 | AD | 2,A | 4,D | 2,D | ∞ | |||
| 3 | ADE | 2,A | 3,E | 4,E | ||||
| 4 | ADEB | 3,E | 4,E | |||||
| 5 | ADEBC | 4,E | ||||||
| 6 | ADEBCF |
Hátrány:
A vonalállapotú útválasztásnál a Flooding miatt nagy forgalom keletkezik. A Flooding végtelen hurkolást okozhat, ez a probléma megoldható a Time-to-leave mező
használatával.
