A standard eltérés egy szám, amely megmondja, hogy egy számhalmaz milyen mértékben tér el egymástól.A standard eltérés 0-tól a végtelenig terjedhet. A 0-ás szórás azt jelenti, hogy a számok listája mind egyenlő – egyáltalán nem térnek el egymástól.
Százalékeltérés – Példa
Öt pályázó egy álláspályázat részeként IQ-tesztet töltött ki. Az alábbiakban az IQ három komponensére kapott pontszámaik láthatók.
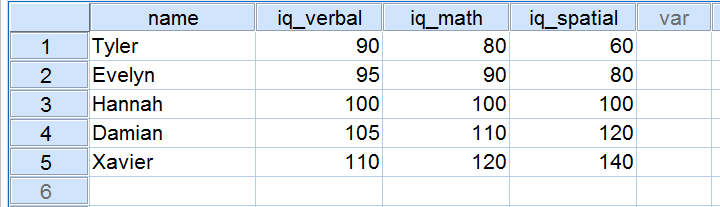
Most nézzük meg közelebbről a 3 IQ komponensre kapott pontszámokat. Vegyük észre, hogy mindháromnak 100 az átlaga az 5 pályázónk esetében. Az iq_verbal pontszámok azonban közelebb helyezkednek el egymáshoz, mint az iq_math pontszámok. Továbbá az iq_spatial pontszámok távolabb helyezkednek el egymástól, mint az első két komponens pontszámai. A pontszámok közötti pontos távolságot számmal lehet kifejezni. Ezt a számot standard eltérésnek nevezzük.
Standard eltérés – eredmények
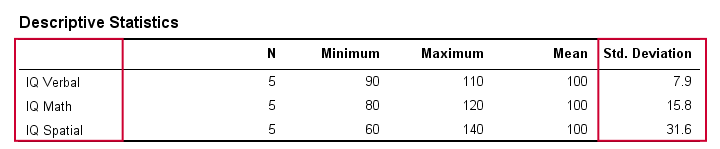
A való életben nyilvánvalóan nem vizsgáljuk vizuálisan a nyers pontszámokat, hogy lássuk, milyen messze vannak egymástól. Ehelyett egyszerűen egy szoftverrel kiszámoltatjuk őket helyettünk (erről később). Az alábbi táblázat az IQ-adataink standard eltéréseit és néhány más statisztikát mutat. Vegyük észre, hogy a szórások megerősítik a nyers adatokban látott mintázatot.
Standardeltérés és hisztogram
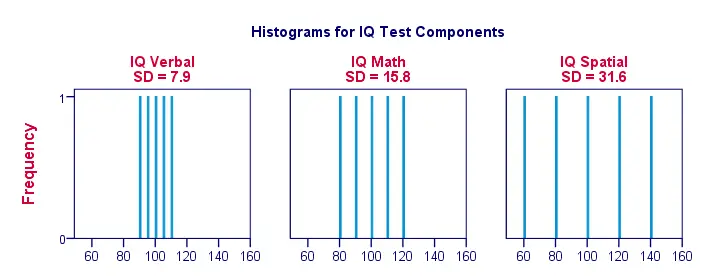
Jól van, tegyük a dolgokat egy kicsit szemléletesebbé. Az alábbi ábra az IQ-eredményeink standard eltéréseit és hisztogramjait mutatja. Vegyük észre, hogy minden egyes sáv 1 pályázó pontszámát jelöli 1 IQ-komponensen. Ismét láthatjuk, hogy a szórások jelzik, hogy a pontszámok milyen mértékben térnek el egymástól.
Standardeltérés – További hisztogramok
Ha csak egy maroknyi megfigyelés adatait vizualizáljuk, mint az előző ábrán, könnyen áttekinthető képet kapunk. Egy reálisabb példa kedvéért az alábbiakban 1000 megfigyelésre vonatkozó hisztogramokat mutatunk be. Fontos, hogy ezek a hisztogramok azonos skálákkal rendelkeznek; mindegyik hisztogram esetében az x-tengelyen egy centiméter körülbelül 40 “IQ komponenspontnak” felel meg.
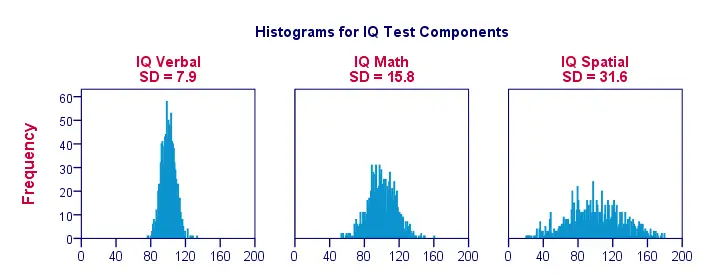
Megjegyezzük, hogy a hisztogramok lehetővé teszik a standard eltérések durva becslését. A “szélesebb” hisztogramok nagyobb standard eltéréseket jeleznek; a pontszámok (x-tengely) távolabb helyezkednek el egymástól. Mivel minden hisztogram azonos felületű (1000 megfigyelésnek megfelelő), a nagyobb szóráshoz “alacsonyabb” hisztogramok is társulnak.
Szabványeltérés – populációs képlet
Hogyan számolja ki a szoftver a szórásokat? Nos, az alapképlet a következő
$$\sigma = \sqrt{\frac{\sum(X – \mu)^2}{N}}$$
ahol
- \(X\) minden egyes külön számot jelöl;
- \(\mu\) az összes szám átlagát és
- \(\sum\) az összeget jelöli.
A szórás tehát az egyes különálló számok és e számok átlaga közötti átlagos négyzetes különbség négyzetgyöke.
Fontos, hogy ez a képlet feltételezi, hogy az adataink tartalmazzák a teljes vizsgált populációt (ezért “populációs képlet”). Ha az adatai csak egy mintát tartalmaznak a célsokaságból, lásd alább.
Populációs képlet – Szoftver
Ezt a képletet a Google sheets, az OpenOffice és az Excel programokban használhatja a =STDEVP(...) beírásával egy cellába. Adja meg a zárójelek között azokat a számokat, amelyek felett a szórást szeretné megkapni, és nyomja meg az Entert. Az alábbi ábra szemlélteti az ötletet.
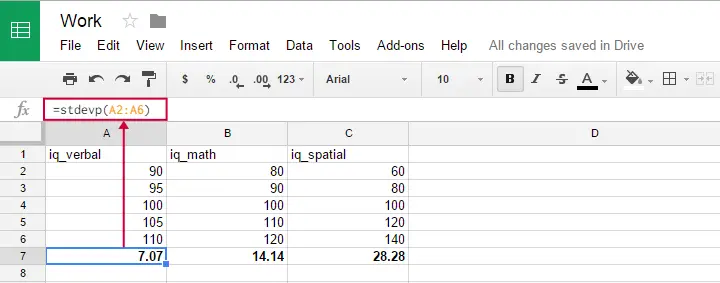
Furcsa, hogy a populáció szórásképlete úgy tűnik, nem létezik az SPSS-ben.
Százalékeltérés – minta képlet
Most valami kihívást jelent: ha az adatai (megközelítőleg) egyszerű véletlen minta valamilyen (sokkal) nagyobb populációból, akkor az előző képlet szisztematikusan alábecsüli a standard eltérést ebben a populációban. A populáció szórásának torzítatlan becslőjét a
$$$S_x = \sqrt{\frac{\sum(X – \overline{X})^2}{N -1}}$$
A számítások tekintetében a nagy különbség az első képlettel szemben az, hogy \(n -1\) helyett \(n\)-vel osztunk. A kisebb számmal való osztás (kissé) nagyobb eredményt eredményez. Ez pontosan kompenzálja a fent említett alulbecslést. Nagy mintanagyság esetén azonban a két képlet gyakorlatilag azonos eredményt ad.
A GoogleSheetsben, az Open Office-ban és az MS Excelben a STDEV függvény ezt a második képletet használja. Ez az SPSS-ben implementált (egyetlen) szórásképlet is.
Szokványeltérés és szórás
A második szám, amely kifejezi, hogy egy számhalmaz milyen messze van egymástól, a szórás. A variancia a standard eltérés négyzete. Ez azt jelenti, hogy a szóráshoz hasonlóan a szórásnak is van egy populációs és egy mintavételi képlete.
Elvileg kínos, hogy két különböző statisztika alapvetően ugyanazt a tulajdonságát fejezi ki egy számhalmaznak. Miért nem dobjuk el a szórást a szórás javára (vagy fordítva)? Az alapvető válasz az, hogy a szórás bizonyos helyzetekben kívánatosabb tulajdonságokkal rendelkezik, más helyzetekben pedig a variancia.
