Dodawanie (lub odejmowanie) ułamków wymaga, aby mianowniki ułamków były równe.
Równe mianowniki
Jeśli mianowniki są równe, suma ułamków jest obliczana przez dodanie liczników i zachowanie mianownika.
Przykład:
Dodajmy 4/7 i 3/7:
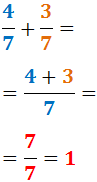 W ten sam sposób oblicza się odejmowanie ułamków o jednakowych mianownikach, odejmując liczniki i zachowując mianownik.
W ten sam sposób oblicza się odejmowanie ułamków o jednakowych mianownikach, odejmując liczniki i zachowując mianownik.
Przykład:
Odejmujemy 4/7 i 3/7:
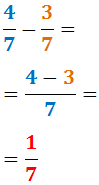
Różne mianowniki
Gdy mianowniki są różne, musimy trochę podziałać, by zamienić ułamki na ułamki równoważne, tak by miały ten sam mianownik.
Wyjaśnijmy procedurę obliczania sumy
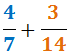
1. Obliczamy najmniejszą wspólną wielokrotność mianowników:
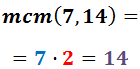
2. W mianowniku każdego ułamka zapisujemy najmniejszą otrzymaną wspólną wielokrotność:
3. W liczniku każdego ułamka zapisujemy wynik dzielenia najmniejszej wspólnej wielokrotności (nowego mianownika) przez początkowy mianownik i mnożenia go przez początkowy licznik: Początkowy mianownik pierwszego ułamka wynosił 7, a początkowy licznik 4:
Początkowy mianownik drugiego ułamka wynosił 14, a początkowy licznik 3:
Tak więc mamy sumę dwóch ułamków o równych mianownikach:
4. Dodajemy ułamki:
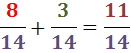
Aby odjąć wykonujemy te same kroki, ale na końcu, zamiast dodawać ułamki, odejmujemy je.
Zasoby ułamków:
- Pojęcie ułamka
- Upraszczanie ułamków
- Ułamki równoważne (1)
- Ułamki równoważne (2)
- Dodawanie i odejmowanie ułamków
- Mnożenie i dzielenie. ułamki
- Ułamki generujące liczby dziesiętne
- Ułamki mieszane
- Problemy z procentami
- Interaktywne ćwiczenia z ułamkami
- Operacje z ułamkami
