Komparator cyfrowy magnitudy jest układ kombinacyjny, który porównuje dwie liczby cyfrowe lub binarne w celu ustalenia, czy jedna liczba binarna jest równa, mniejsza lub większa od drugiej liczby binarnej. Logicznie projektujemy obwód, dla którego będziemy mieli dwa wejścia jedno dla A i drugie dla B i mamy trzy wyjścia, jedno dla A > B warunek, jedno dla A = B warunek i jedno dla A < B warunek.
Komparator wielkości 1-bitowej –
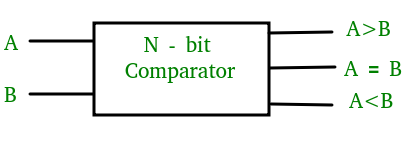
Komparator służący do porównywania dwóch bitów nazywany jest komparatorem jednobitowym. Składa się on z dwóch wejść, każde dla dwóch liczb jednobitowych i trzech wyjść do generowania mniej niż, równych i większych niż pomiędzy dwoma liczbami binarnymi.
Tablica prawdy dla komparatora 1-bitowego jest podana poniżej:
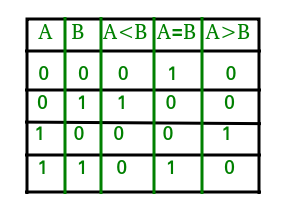
Z powyższej tabeli prawdy wyrażenia logiczne dla każdego wyjścia można wyrazić następująco:
A>B: AB'A<B: A'BA=B: A'B' + AB
Z powyższych wyrażeń możemy wyprowadzić następujący wzór:

Używając tych wyrażeń logicznych, możemy zaimplementować obwód logiczny dla tego komparatora, jak podano poniżej:
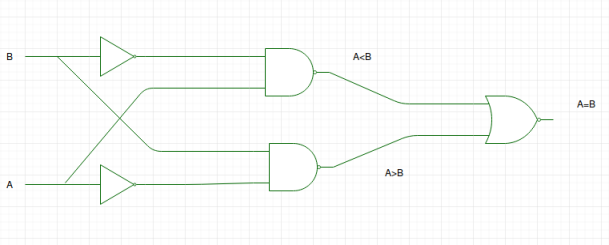
Schemat logiczny jest błędny
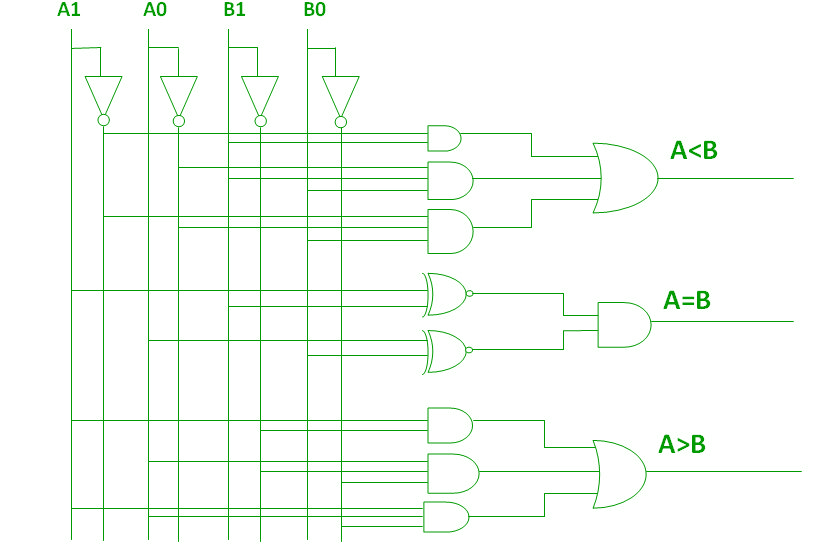
Komparator 2-bitowej wielkości –
Komparator używany do porównywania dwóch liczb binarnych, z których każda ma dwa bity, nazywany jest komparatorem 2-bitowej wielkości. Składa się on z czterech wejść i trzech wyjść do generowania mniej niż, równych i większych niż pomiędzy dwoma liczbami binarnymi.
Tablica prawdy dla 2-bitowego komparatora jest podana poniżej:
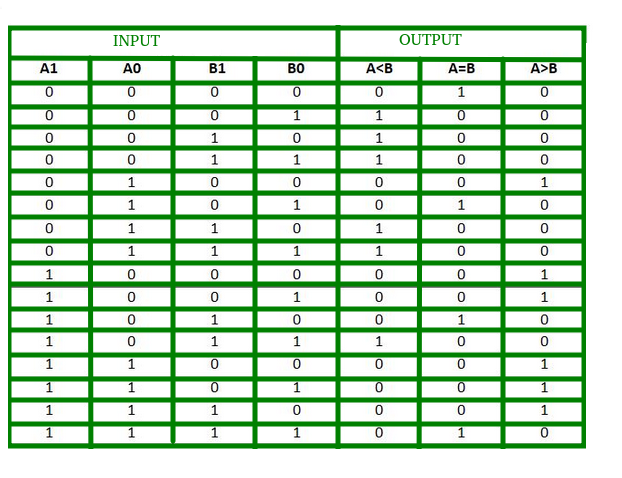
Z powyższej tablicy prawdy K-mapę dla każdego wyjścia można narysować w następujący sposób:



Z powyższych K-map wyrażenia logiczne dla każdego wyjścia można wyrazić następująco:
A>B:A1B1' + A0B1'B0' + A1A0B0'A=B: A1'A0'B1'B0' + A1'A0B1'B0 + A1A0B1B0 + A1A0'B1B0' : A1'B1' (A0'B0' + A0B0) + A1B1 (A0B0 + A0'B0') : (A0B0 + A0'B0') (A1B1 + A1'B1') : (A0 Ex-Nor B0) (A1 Ex-Nor B1)A<B:A1'B1 + A0'B1B0 + A1'A0'B0
Używając tych wyrażeń logicznych, możemy zaimplementować obwód logiczny dla tego komparatora, jak podano poniżej:
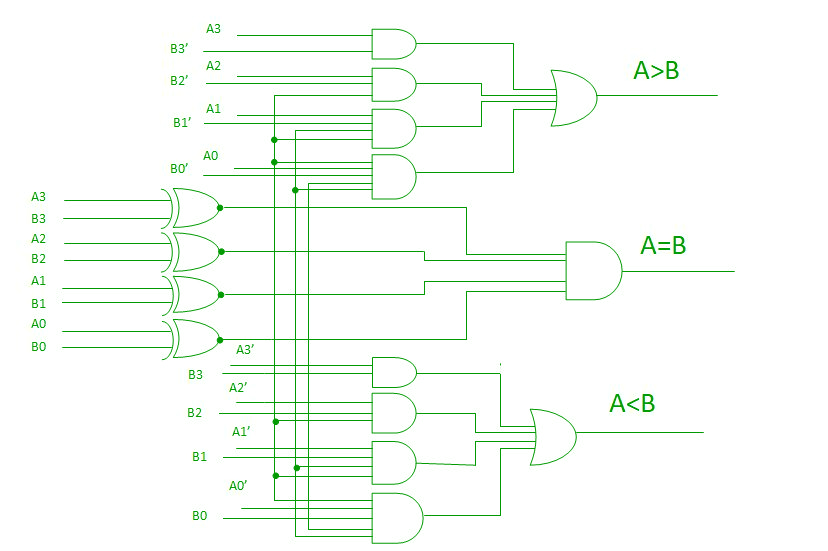
4-Bit Magnitude Comparator –
Komparator używany do porównywania dwóch liczb binarnych po cztery bity nazywamy 4-bitowym komparatorem magnitudy. Składa się on z ośmiu wejść, każde dla dwóch liczb czterobitowych i trzech wyjść do generowania mniej niż, równych i większych niż pomiędzy dwoma liczbami binarnymi.
W komparatorze 4-bitowym spełnienie warunku A>B jest możliwe w czterech następujących przypadkach:
- Jeśli A3 = 1 i B3 = 0
- Jeśli A3 = B3 i A2 = 1 i B2 = 0
- Jeśli A3 = B3, A2 = B2 i A1 = 1 i B1 = 0
- Jeśli A3 = B3, A2 = B2, A1 = B1 oraz A0 = 1 i B0 = 0
Podobnie warunek dla A<B może być możliwy w następujących czterech przypadkach:
- Jeśli A3 = 0 i B3 = 1
- Jeśli A3 = B3 i A2 = 0 i B2 = 1
- Jeśli A3 = B3, A2 = B2 i A1 = 0 i B1 = 1
- Jeśli A3 = B3, A2 = B2, A1 = B1 i A0 = 0 i B0 = 1
Warunek A=B jest możliwy tylko wtedy, gdy wszystkie poszczególne bity jednej liczby dokładnie pokrywają się z odpowiadającymi im bitami innej liczby.
Z powyższych stwierdzeń wynika, że wyrażenia logiczne dla każdego wyjścia mogą być wyrażone następująco:
AA, 831331 r: (A3 EioNor 33)A2132′ a (A3 Ex-Nor 133) (A2 Ex-Nor 132)A131′ a (A3 Ex-Nor 33) (A2 ENor132) (Al Ex-Nor 31)A01301
,13: A3’03 a (A3 Ex-Nor 33)A211:12 a (A3 Ex-Nor 83) (A2 Ex-Nor 132)Ar131 a (A3 Ex-Nor 33) (A2 Ex-Nor32) (Al Ex-Nor 131)A0N30
A=B: (A3 Ex-Nor B3) (A2 Ex-Nor 82) (Al Ex-Nor BI) (AO Ex-Nor BO)
Używając tych wyrażeń boole’owskich, możemy zaimplementować obwód logiczny dla tego komparatora, jak podano poniżej:
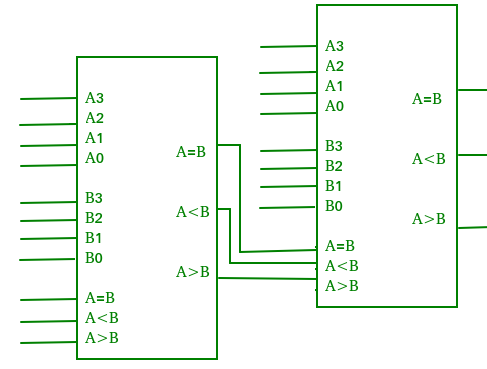
Komparator kaskadowy –
Komparator wykonujący operację porównania do więcej niż czterech bitów poprzez kaskadowanie dwóch lub więcej komparatorów 4-bitowych nazywamy komparatorem kaskadowym. Gdy dwa komparatory mają być kaskadowane, wyjścia komparatora niższego rzędu są połączone z odpowiednimi wejściami komparatora wyższego rzędu.
Zastosowania komparatorów –
- Komparatory są stosowane w jednostkach centralnych (CPU) i mikrokontrolerach (MCU).
- Są one wykorzystywane w aplikacjach sterujących, w których liczby binarne reprezentujące zmienne fizyczne, takie jak temperatura, położenie itp. są porównywane z wartością odniesienia.
- Komparatory są również wykorzystywane jako sterowniki procesów i do sterowania silnikami Servo.
- Używane w weryfikacji haseł i aplikacjach biometrycznych.
.
