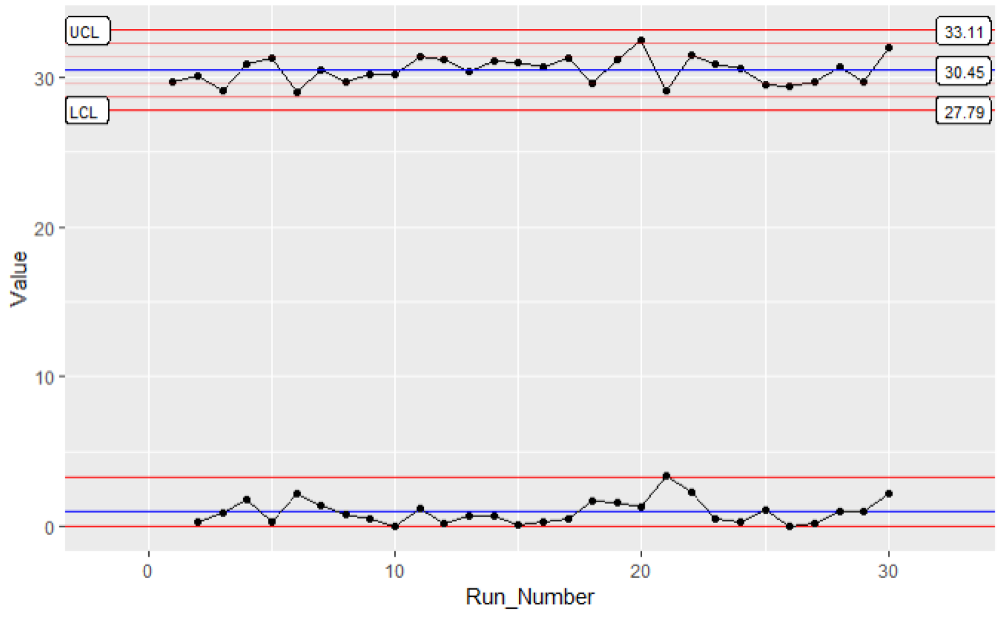
Pakiet ggQC jest rozszerzeniem kontroli jakości dla ggplot. Za jego pomocą można tworzyć wykresy kontrolne XmR, XbarR, C i wiele innych, które można dostosować do własnych potrzeb. Dodatkowe funkcje statystycznej kontroli procesu obejmują kontrole naruszenia Shewarta, jak również analizę zdolności. Jeśli Twój proces przebiega bezproblemowo, zwizualizuj potencjalny wpływ kolejnego usprawnienia procesu za pomocą wykresu Pareto. Aby dowiedzieć się więcej, czytaj dalej!
Aby rozpocząć pracę z ggQC, zainstaluj go z CRAN, uruchamiając następujący kod:
1 |
install.packages("ggQC")
|
wykresy kontrolne ggQC
Wykresy kontrolne są doskonałym sposobem na monitorowanie wyników procesu, wprowadzanie ulepszeń i ocenę systemów pomiarowych. Typy wykresów kontrolnych obsługiwane przez ggQC obejmują:
- Wykresy indywidualne : mR, XmR
- Wykresy atrybutów : c, np, p, u
- Wykresy uczące: xBar.rBar, xBar.rMedian, xBar.sBar, xMedian.rBar, xMedian.rMedian
- Wykresy rozproszenia: rBar, rMedian, sBar
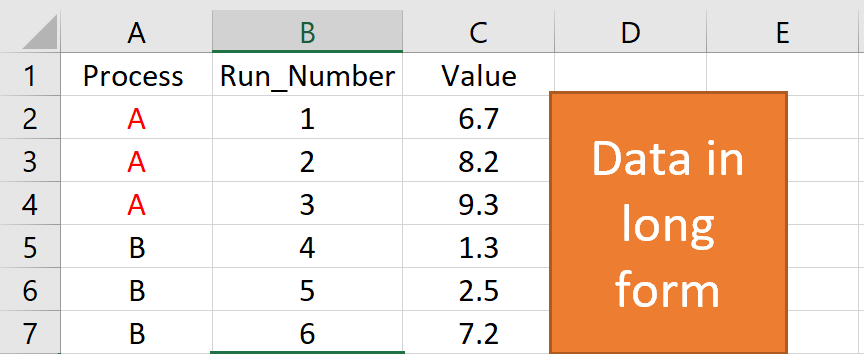
Proces budowania wykresów kontrolnych za pomocą ggQC jest prosty. Po pierwsze, załaduj biblioteki ggQC i ggplot2. Następnie należy załadować dane do R. Dane powinny być w formacie długim. Poniższy zestaw danych jest przykładem danych długoformatowych, jeśli nie jesteś zaznajomiony z tym terminem.
Na koniec wykonaj wykres kontrolny, używając standardowej składni ggplot warstwa po warstwie i polecenia stat_QC(). Poniższy przykładowy kod pokazuje, jak wszystkie te kroki składają się na wykres XmR.
1234567891011121314151617181920212223242526 |
## Załaduj potrzebne bibliotekilibrary(ggplot2)library(ggQC) ### Przygotuj dane demo (zamiast tego załaduj swój plik tutaj)set.seed(5555)Process_Data <- data.frame( Process=rep(c("A"), each = 30), #Process A Run_Number=c(1:30), #Run Order Value = c(rnorm(n = 30, mean = 30.5, sd = 1)) #Process A Random Data ) ### Make the plotXmR_Plot <- ggplot(Process_Data, aes(x = Run_Number, y = Value)) + #init ggplot geom_point() + geom_line() + # dodaj punkty i linie stat_QC(method = "XmR", # określ metodę wykresów QC auto.label = T, # użyj autolabels label.digits = 2, # użyj dwóch cyfr w etykiecie show.1n2.sigma = T # pokaż 1 i dwie linie sigma ) + scale_x_continuous(expand = expand_scale(mult = .15)) # Pad the x-axis ### Draw the plot - DoneXmR_Plot
|
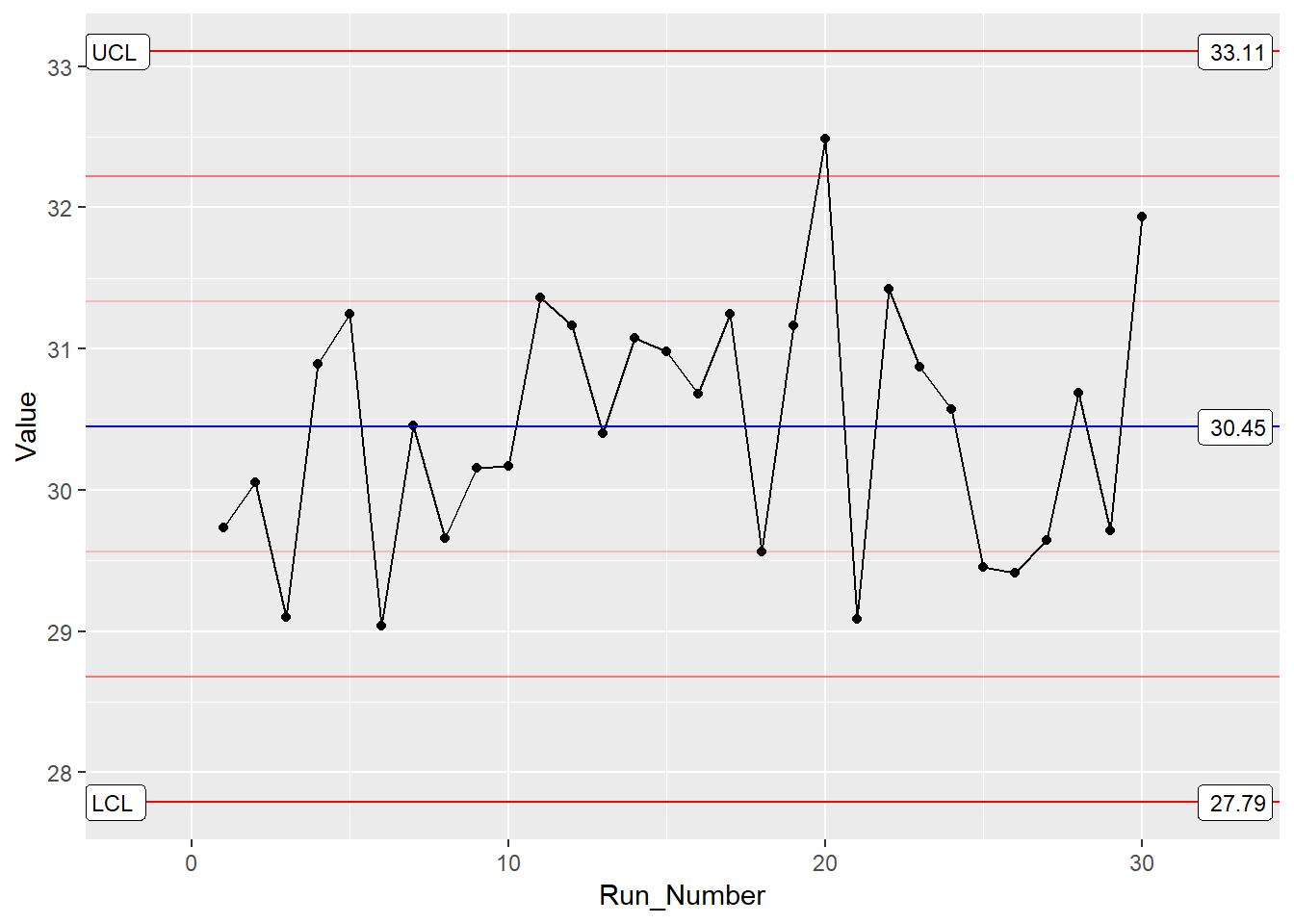
By opierać się na frameworku ggplot, otrzymujemy wysoki poziom kontroli nad szczegółami wykresu, takimi jak punkty i linie itp. Dodatkowo, jeśli chcesz umieścić dane XmR i mR na tej samej działce, możesz to zrobić. Wystarczy wykonać wiele wywołań polecenia stat_QC(), jak pokazano poniżej.
1234567891011121314 |
## Dwa wywołania stat_QCXmR_Plot <- ggplot(Process_Data, aes(x = Run_Number, y = Value)) + #init ggplot geom_point() + geom_line() + #add the points and lines stat_QC(method = "XmR", #specify QC charting method auto.label = T, #Użyj autolabels label.digits = 2, #Użyj dwóch cyfr w etykiecie show.1n2.sigma = T #Pokaż 1 i dwie linie sigma ) + stat_QC(method="mR") + scale_x_continuous(expand = expand_scale(mult = .15)) # Pad the x-axis ### Draw the plot - DoneXmR_Plot |
Aby uzyskać więcej przykładów wykresów kontrolnych, sprawdź docs, HOWTOs, and Vignettes na rcontrolcharts.com.
Analiza naruszeń
Aby sprawdzić, czy w twoim procesie nie ma danych poza kontrolą, użyj polecenia stat_qc_violations(). Po uruchomieniu tego polecenia dane są sprawdzane pod kątem następujących 4 reguł naruszeń Shewarta:
- Same Side: 8 lub więcej kolejnych punktów po tej samej stronie
- 1 Sigma: 4 lub więcej kolejnych punktów po tej samej stronie przekraczających 1 sigma
- 2 Sigma: 2 lub więcej kolejnych punktów po tej samej stronie przekraczających 2 sigma
- 3 Sigma: dowolne punkty przekraczające 3 sigma
Kolejny fragment kodu demonstruje analizę naruszeń za pomocą polecenia stat_qc_violation() z wykorzystaniem danych procesu z poprzedniej sekcji.
12345678 |
#Używa tych samych danych co poprzedni przykład. QC_Violations <- ggplot(Process_Data, aes(x = Run_Number, y = Value)) + #init ggplot stat_qc_violations(method = "XmR" #show.facets = 4 #if you just want facet 4 )QC_Violations |
Po wykonaniu kodu powinieneś zobaczyć wykres z 4 fasetami – po jednej dla każdej reguły Shewarta. Jeśli chcemy zobaczyć tylko 4 fasety, ustawiamy show.facets = 4. Inne ustawienia, takie jak show.facets = c(2, 4) spowodują wyświetlenie tylko naruszeń 1 i 3 sigma.
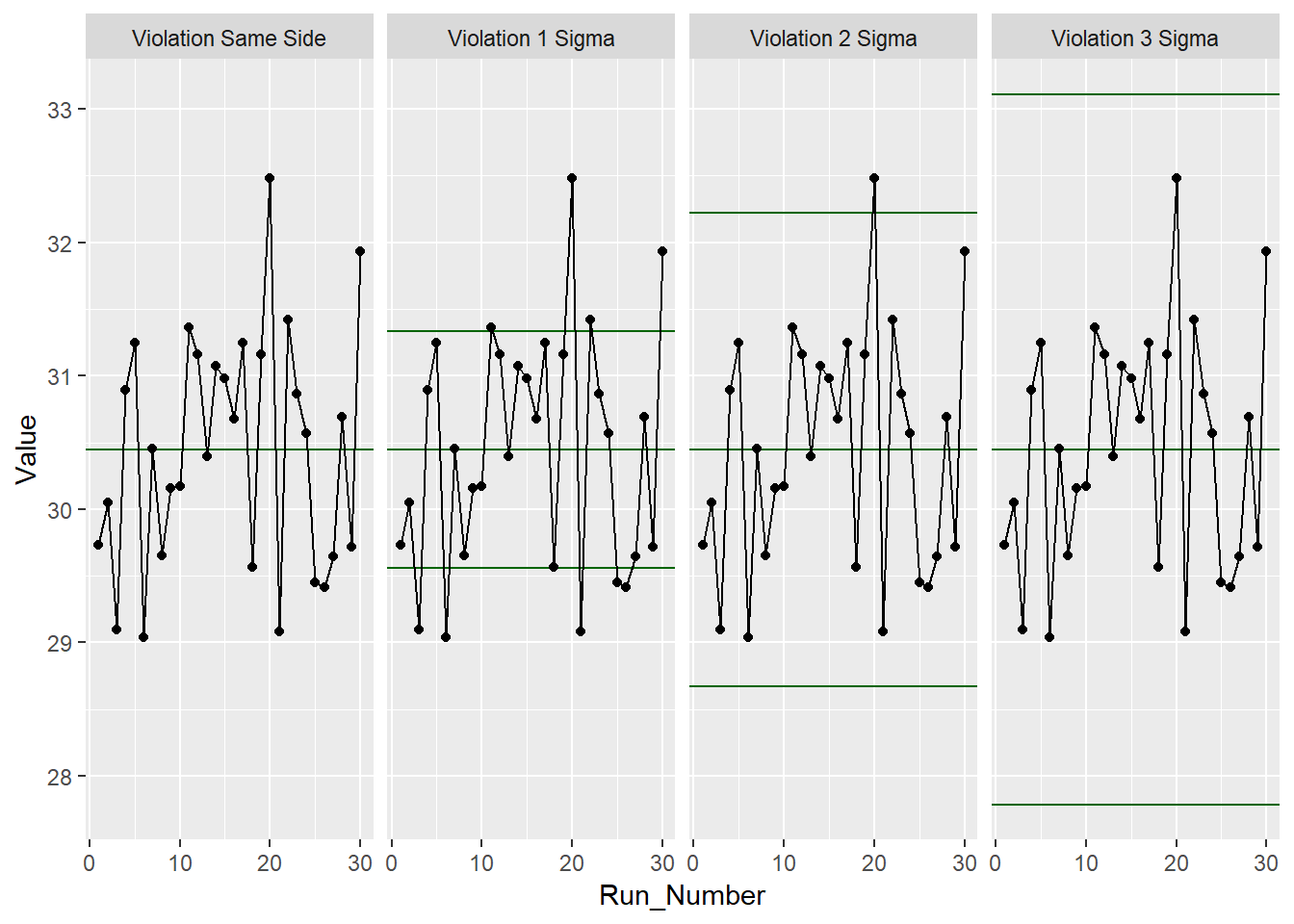
W przypadku naszych danych testowych nie zaobserwowano żadnego ze standardowych 4 naruszeń reguły Shewarta. Super! Następnie przyjrzymy się analizie zdolności przy użyciu ggQC.
Analiza zdolności
W poprzednich rozdziałach dowiedziałeś się, jak stworzyć wykres kontrolny za pomocą ggQC i sprawdzić, czy nie doszło do naruszeń. Tutaj dowiesz się, jak wykonać podstawową analizę zdolności (Cp, Cpk, Pp, Ppk itd.). W tym celu zakładamy, że klient ma dolną granicę specyfikacji (LSL) i górną granicę specyfikacji (USL) wynoszące odpowiednio 25 i 37. Mając te specyfikacje i polecenie stat_QC_Capability(), możesz wykonać graficzną analizę zdolności w kilku prostych liniach kodu:
12345678910111213 |
# Używa tych samych danych co pierwszy przykładCapabilityAnaylsis <- ggplot(Process_Data, aes(x = Value)) + #init ggplot geom_histogram(binwidth = .75, color="purple") + #make the histogram stat_QC_Capability( LSL=25, USL=37, #Specify LSL and USL show.cap.summary = c("Cp", "Cpk"), #wybrane podsumowanie digits = 2, #podaj dwie cyfry method="XmR") + #wykorzystaj metody XmR metodcale_x_continuous(expand = expand_scale(mult = c(0.15,.65))) #pad the X-axis #plot the graphCapabilityAnaylsis
|
Aby dostosować metryki zdolności wyświetlane na wykresie, podaj argument show.cap.summary z wektorem pożądanych metryk. Dostępne metryki obejmują:
- TOL: Tolerancja w jednostkach sigma (USL-LSL)/sigma
- DNS: Distance to Nearest Specification Limit in Sigma Units
- Cp: Cp (Within sample elbow-room metric)
- Cpk: Cpk (W obrębie metryki centrowania próbki)
- Pp: Pp (Between sample elbow-room metric)
- Ppk: Ppk (Between sample centering metric)
- LCL: Lower Control Limit
- X: Process Center
- UCL: Upper Control Limit
- Sig: Sigma z wykresów kontrolnych
Kolejność podana w wektorze jest kolejnością wyświetlaną na wykresie. W tym przypadku zostały wybrane tylko Cp i Cpk, jak pokazano poniżej.
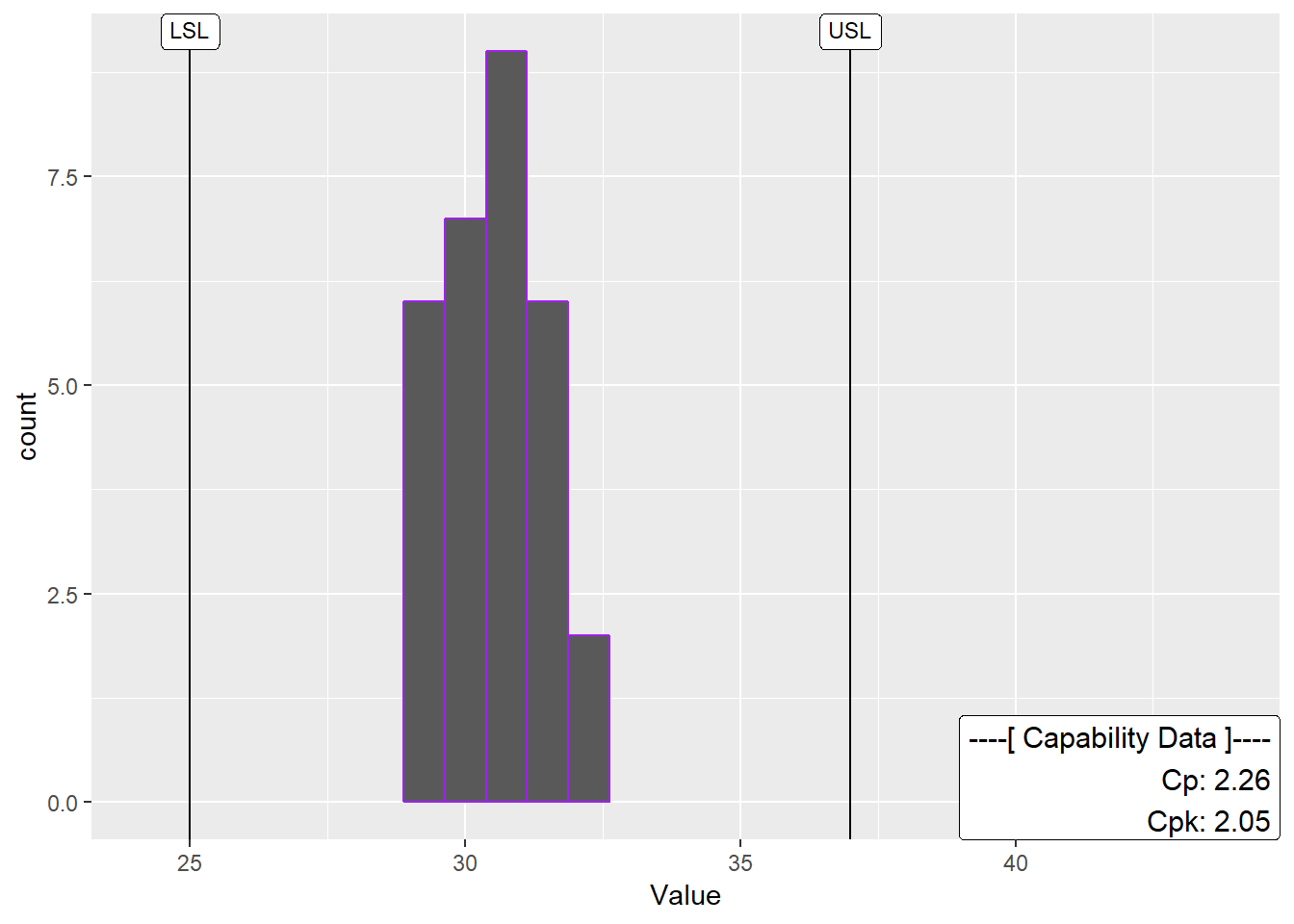
Cool! Wygląda na to, że proces jest w dobrej kondycji. Aby zobaczyć więcej przykładów analizy wydolności, zapoznaj się z dokumentacją ggQC i przykładami stat_QC_Capability. stat_QC_Capability jest również kompatybilne z facetingiem ggplot. Zauważ, że wykresy zdolności XbarR są określone nieco inaczej niż XmR.
Analiza Pareto
W porządku, więc twoje procesy są pod kontrolą. Wiadomo jednak, że w procesie występują wąskie gardła. Od czego należy zacząć? Jednym ze sposobów, który pomoże zaplanować atak, jest analiza Pareto. Załóżmy, że dysponujemy następującymi danymi pokazującymi, jak długo trwa kilka typowych etapów procesu.
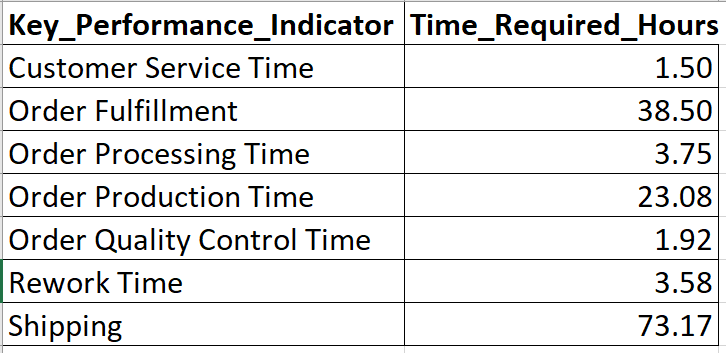
Aby wygenerować wykres Pareto, załaduj dane, zainicjalizuj ggplot i pozwól poleceniu stat_pareto() zrobić resztę.
12345678910111213141516171819 |
#wczytaj swoje daneData4Pareto <- data.frame( KPI = c("Customer Service Time", "Order Fulfillment", "Order Processing Time", "Order Production Time", "Order Quality Control Time", "Rework Time", "Shipping"), Time = c(1.50, 38.50, 3.75, 23.08, 1.92, 3.58, 73.17)) #make the plotggplot(Data4Pareto, aes(x=KPI, y=Time)) + stat_pareto(point.color = "red", point.size = 3, line.color = "black", bars.fill = c("blue", "orange") ) + theme(axis.text.x = element_text(angle = 90, hjust = 1, vjust=0.5)) #done
|
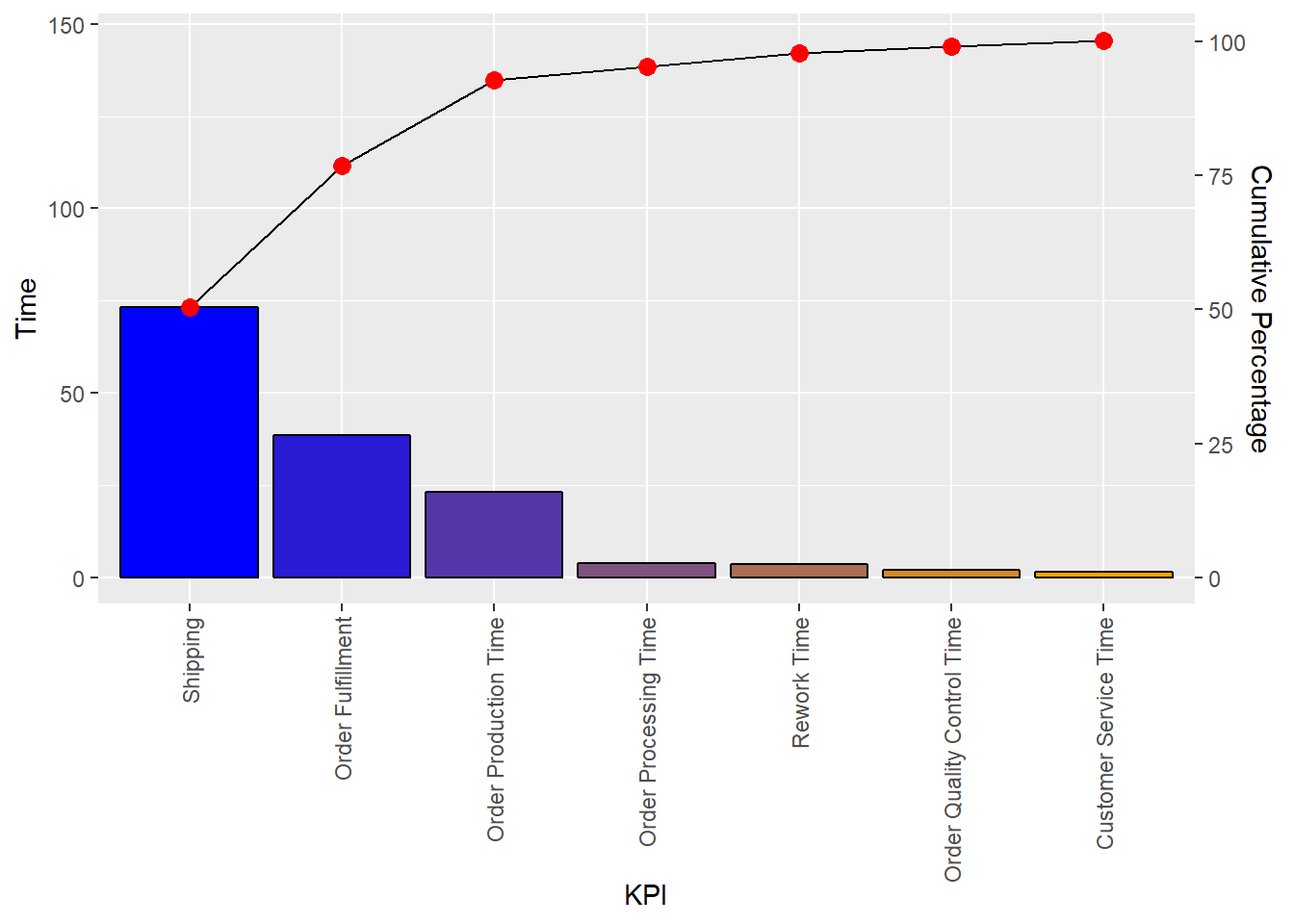
Wygląda na to, że nasz następny projekt poprawy skupi się na wysyłce lub realizacji zamówień. Powodzenia!
Podsumowanie
Budowanie wykresów kontrolnych za pomocą ggQC jest szybkie i łatwe, zwłaszcza jeśli użytkownik jest już zaznajomiony z ggplot. Podobnie jak inne wykresy ggplot, wykresy kontrolne ggQC obsługują fasetowanie i są budowane warstwa po warstwie. Jeśli potrzebujesz stworzyć skomplikowany wykres, proszę bardzo. Możesz dodać tyle wywołań stat_QC, ile chcesz (zobacz XbarR_Vignette). Oprócz wykresów kontrolnych, ggQC pozwala na przeprowadzanie analiz Pareto, zdolności i naruszeń Shewarta. Aby dowiedzieć się więcej, proszę odwiedzić rcontrolcharts.com
Inne użyteczne linki
- Wyjaśnienie stałych wykresu kontrolnego
.