Kilka lat temu, Scott Fortmann-Roe napisał świetny esej zatytułowany „Understanding the Bias-Variance Tradeoff.”
As data science morphs into an accepted profession with its own set of tools, procedures, workflows, etc., często wydaje się, że mniej uwagi poświęca się procesom statystycznym na rzecz bardziej ekscytujących aspektów (zobacz tutaj i tutaj parę przykładowych dyskusji).
Definicje pojęciowe
Chociaż będzie to służyć jako przegląd eseju Scotta, który można przeczytać dla dalszych szczegółów i wglądów matematycznych, zaczniemy od dosłownych definicji Fortmanna-Roe’a, które są centralne dla kawałka:
Błąd spowodowany uprzedzeniem: Błąd spowodowany uprzedzeniem jest brany jako różnica między oczekiwanym (lub średnim) przewidywaniem naszego modelu a prawidłową wartością, którą próbujemy przewidzieć. Oczywiście masz tylko jeden model, więc mówienie o oczekiwanych lub średnich wartościach predykcji może wydawać się nieco dziwne. Wyobraź sobie jednak, że możesz powtarzać cały proces budowania modelu więcej niż raz: za każdym razem zbierasz nowe dane i przeprowadzasz nową analizę, tworząc nowy model. Ze względu na losowość w bazowych zestawach danych, wynikowe modele będą miały zakres przewidywań. Skośność mierzy, jak daleko przewidywania tych modeli są od poprawnej wartości.
Błąd z powodu wariancji: Błąd ze względu na wariancję jest brany jako zmienność przewidywań modelu dla danego punktu danych. Ponownie, wyobraź sobie, że możesz powtórzyć cały proces budowy modelu wiele razy. Wariancja jest tym, jak bardzo przewidywania dla danego punktu różnią się między różnymi realizacjami modelu.
Podstawowo, stronniczość jest tym, jak bardzo przewidywania modelu są oddalone od poprawności, podczas gdy wariancja jest stopniem, do którego te przewidywania różnią się między iteracjami modelu.
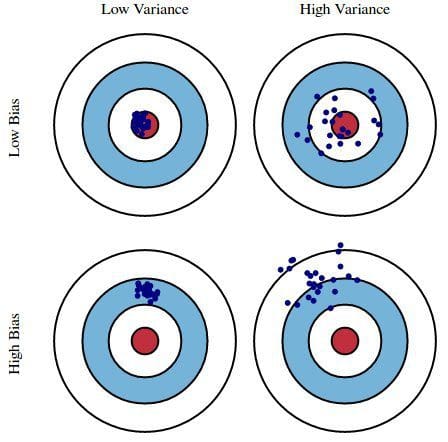
Rys. 1: Graficzna ilustracja błędu systematycznego i wariancji
Z książki Understanding the Bias-Variance Tradeoff, autorstwa Scotta Fortmanna-Roe.
Dyskusja
Używając prostego, wadliwego sondażu dotyczącego wyborów prezydenckich jako przykładu, błędy w sondażu są następnie wyjaśnione przez bliźniacze soczewki błędu systematycznego i wariancji: wybór uczestników sondażu z książki telefonicznej jest źródłem błędu systematycznego; mała wielkość próby jest źródłem wariancji; minimalizacja całkowitego błędu modelu polega na zrównoważeniu błędów błędu systematycznego i wariancji.
Fortmann-Roe następnie przechodzi do omówienia tych kwestii, ponieważ odnoszą się one do pojedynczego algorytmu: k-Nearest Neighbor. Następnie przedstawia kilka kluczowych kwestii do przemyślenia przy zarządzaniu błędem systematycznym i wariancją, w tym techniki ponownego próbkowania, asymptotyczne właściwości algorytmów i ich wpływ na błędy systematycznego próbkowania i wariancji oraz zwalczanie swoich założeń zarówno w odniesieniu do danych, jak i ich modelowania. Moim zdaniem, tutaj jest najważniejszy punkt:
Jak coraz więcej parametrów jest dodawanych do modelu, złożoność modelu wzrasta i wariancja staje się naszym głównym problemem, podczas gdy uprzedzenie stale spada. Na przykład, im więcej terminów wielomianowych dodaje się do regresji liniowej, tym większa będzie złożoność modelu wynikowego. Innymi słowy, skośność ma ujemną pochodną pierwszego rzędu w odpowiedzi na złożoność modelu, podczas gdy wariancja ma dodatnie nachylenie.

Rys. 2: Skośność i wariancja przyczyniające się do całkowitego błędu
Z książki Understanding the Bias-Variance Tradeoff, autorstwa Scotta Fortmanna-Roe.
Fortmann-Roe kończy sekcję o nadmiernym i niedostatecznym dopasowaniu wskazując na inny ze swoich świetnych esejów (Accurately Measuring Model Prediction Error), a następnie przechodzi do wysoce zgodnego zalecenia, że „miary oparte na próbkowaniu, takie jak walidacja krzyżowa, powinny być preferowane w stosunku do miar teoretycznych, takich jak kryteria informacyjne Aikake’a.”
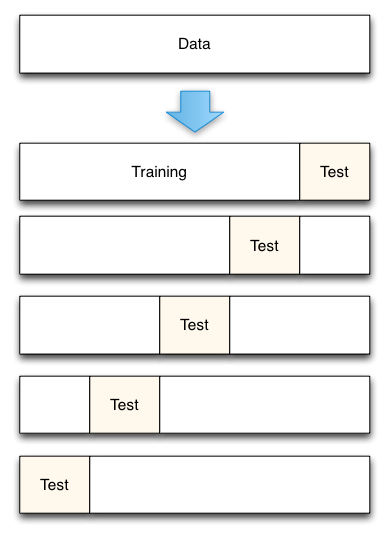
Fig. 3: 5-krotna walidacja krzyżowa podziału danych
From Accurately Measuring Model Prediction Error, autorstwa Scotta Fortmanna-Roe.
Oczywiście, w przypadku walidacji krzyżowej, liczba fałd do wykorzystania (k-krotna walidacja krzyżowa, prawda?), wartość k jest ważną decyzją. Im niższa wartość, tym większa skośność w szacunkach błędów i mniejsza wariancja. I odwrotnie, gdy k jest równe liczbie instancji, oszacowanie błędu ma wtedy bardzo niską skośność, ale może mieć wysoką wariancję. W przypadku nawet najbardziej rutynowych metod oceny statystycznej, takich jak k-krotna walidacja krzyżowa, kompromis pomiędzy stronniczością a wariancją jest bardzo ważny do zrozumienia.
Niestety, walidacja krzyżowa wydaje się również, czasami, tracić swój urok w nowoczesnej erze nauki o danych, ale jest to dyskusja na inny czas.
Polecam przeczytanie całego eseju Scotta Fortmanna-Roe na temat kompromisu między tendencyjnością a wariancją, jak również jego fragmentu na temat pomiaru błędu predykcji modelu.
Powiązane:
- Big Data, Bible Codes, and Bonferroni
- Data Science of Variable Selection: A Review
- Datasets Over Algorithms
.
