Link State Routing jest techniką, w której każdy router dzieli się wiedzą o swoim sąsiedztwie z każdym innym routerem w sieci internetowej.
Trzy klucze do zrozumienia algorytmu Link State Routing:
- Wiedza o sąsiedztwie: Zamiast wysyłać swoją tablicę routingu, router wysyła informacje tylko o swoim sąsiedztwie. Router rozgłasza swoje tożsamości i koszt bezpośrednio dołączonych linków do innych routerów.
- Flooding: Każdy router wysyła informacje do każdego innego routera w sieci Internetwork z wyjątkiem swoich sąsiadów. Proces ten jest znany jako Flooding. Każdy router, który otrzyma pakiet, wysyła jego kopie do wszystkich swoich sąsiadów. W końcu każdy router otrzymuje kopię tej samej informacji.
- Udostępnianie informacji: Router wysyła informację do każdego innego routera tylko wtedy, gdy następuje zmiana w informacji.
Link State Routing ma dwie fazy:
Reliable Flooding
- Stan początkowy: Każdy węzeł zna koszt swoich sąsiadów.
- Stan końcowy: Każdy węzeł zna cały graf.
Obliczanie tras
Każdy węzeł używa algorytmu Dijkstry na grafie, aby obliczyć optymalne trasy do wszystkich węzłów.
- Algorytm routingu stanu łącza jest również znany jako algorytm Dijkstry, który jest używany do znalezienia najkrótszej ścieżki od jednego węzła do każdego innego węzła w sieci.
- Algorytm Dijkstry jest iteracyjny i ma tę własność, że po k-tej iteracji algorytmu ścieżki najmniejszego kosztu są dobrze znane dla k węzłów docelowych.
Opiszmy kilka pojęć:
- c( i , j): Koszt połączenia z węzła i do węzła j. Jeśli węzły i i j nie są bezpośrednio połączone, to c(i , j) = ∞.
- D(v): Określa koszt ścieżki od kodu źródłowego do docelowego v, która ma aktualnie najmniejszy koszt.
- P(v): Określa poprzedni węzeł (sąsiad v) wraz z aktualną ścieżką o najmniejszym koszcie od źródła do v.
- N: Jest to całkowita liczba węzłów dostępnych w sieci.
Algorytm
InitializationN = {A} // A is a root node.for all nodes vif v adjacent to Athen D(v) = c(A,v)else D(v) = infinityloopfind w not in N such that D(w) is a minimum.Add w to NUpdate D(v) for all v adjacent to w and not in N:D(v) = min(D(v) , D(w) + c(w,v))Until all nodes in N
W powyższym algorytmie po kroku inicjalizacji następuje pętla. Liczba powtórzeń pętli jest równa całkowitej liczbie węzłów dostępnych w sieci.
Zrozumiejmy to na przykładzie:
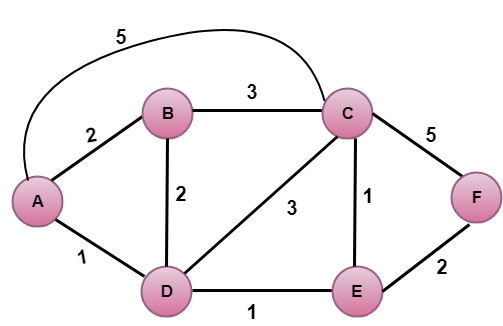
Na powyższym rysunku wierzchołek źródłowy to A.
Krok 1:
Pierwszym krokiem jest krok inicjalizacji. Obecnie znane najmniej kosztowne ścieżki z A do jego bezpośrednio dołączonych sąsiadów, B, C, D wynoszą odpowiednio 2,5,1. Koszt z A do B jest ustawiony na 2, z A do D jest ustawiony na 1, a z A do C jest ustawiony na 5. Koszty z A do E i F są ustawione na nieskończoność, ponieważ nie są one bezpośrednio powiązane z A.
| Krok | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
Krok 2:
W powyższej tabeli zauważamy, że wierzchołek D zawiera ścieżkę o najmniejszym koszcie w kroku 1. Dlatego jest on dodany w N. Teraz musimy wyznaczyć najmniej kosztowną ścieżkę przez wierzchołek D.
a) Obliczenie najkrótszej ścieżki z A do B
b) Obliczenie najkrótszej ścieżki z A do C
c) Obliczenie najkrótszej ścieżki z A do E
Uwaga: Wierzchołek D nie ma bezpośredniego połączenia z wierzchołkiem E. Dlatego wartość D(F) jest nieskończona.
| Krok | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
| 2 | AD | 2,A | 4,D | 2,D | ∞ |
Krok 3:
W powyższej tabeli obserwujemy, że zarówno E jak i B mają ścieżkę o najmniejszym koszcie w kroku 2. Rozważmy wierzchołek E. Teraz wyznaczamy najmniej kosztowną ścieżkę pozostałych wierzchołków przez E.
a) Obliczenie najkrótszej ścieżki z A do B.
b) Obliczenie najkrótszej ścieżki z A do C.
c) Obliczenie najkrótszej ścieżki z A do F.
| Krok | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | |
| 3 | ADE | 2,A | 3,E | 4,E |
Krok 4:
W powyższej tabeli obserwujemy, że wierzchołek B ma najmniej kosztowną ścieżkę w kroku 3. Dlatego jest on dodawany w N. Teraz wyznaczamy najmniej kosztowną ścieżkę pozostałych wierzchołków przez B.
a) Obliczenie najkrótszej ścieżki z A do C.
b) Obliczenie najkrótszej ścieżki z A do F.
| Krok | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | |
| 3 | ADE | 2,A | 3,E | 4,E | ||
| 4 | ADEB | 3,E | 4,E |
Krok 5:
W powyższej tabeli obserwujemy, że wierzchołek C ma najmniej kosztowną ścieżkę w kroku 4. Dlatego jest on dodawany do N. Teraz wyznaczamy najmniej kosztowną ścieżkę pozostałych wierzchołków przez C.
a) Obliczanie najkrótszej ścieżki z A do F.
| Krok | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | |
| 3 | ADE | 2,A | 3,E | 4,E | ||
| 4 | ADEB | 3,E | 4,E | |||
| 5 | ADEBC | 4,E |
Tabela końcowa:
| Krok | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | |
| 3 | ADE | 2,A | 3,E | 4,E | ||
| 4 | ADEB | 3,E | 4,E | |||
| 5 | ADEBC | 4,E | ||||
| 6 | ADEBCF |
Wady:
Ważny ruch jest tworzony w routingu stanu Line z powodu Flooding. Flooding może powodować nieskończoną pętlę, ten problem można rozwiązać za pomocą pola Time-to-leave
.
