Odchylenie standardowe – co to jest?

Odchylenie standardowe jest liczbą, która mówi nam
do jakiego stopnia zbiór liczb jest od siebie oddalony.Odchylenie standardowe może mieć zakres od 0 do nieskończoności. Odchylenie standardowe równe 0 oznacza, że wszystkie liczby na liście są równe – nie różnią się od siebie w żadnym stopniu.

Odchylenie standardowe – przykład

Pięciu kandydatów wykonało test IQ jako część podania o pracę. Ich wyniki na trzech składowych IQ są pokazane poniżej.

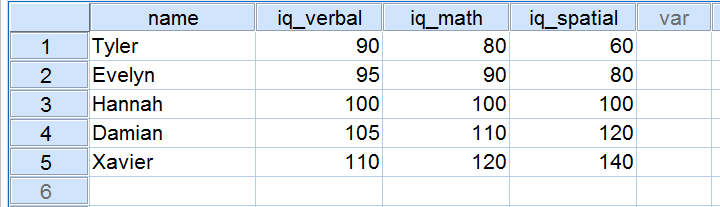
Przyjrzyjmy się teraz dokładnie wynikom na trzech składowych IQ. Zauważ, że wszystkie trzy mają średnią 100 dla naszych 5 kandydatów. Jednakże, wyniki iq_verbal leżą bliżej siebie niż wyniki iq_math. Co więcej, wyniki w iq_spatial leżą dalej od siebie niż wyniki w pierwszych dwóch składowych. Dokładny zakres, w jakim kilka wyników jest od siebie oddalonych, może być wyrażony jako liczba. Ta liczba jest znana jako odchylenie standardowe.

Odchylenie standardowe – Wyniki

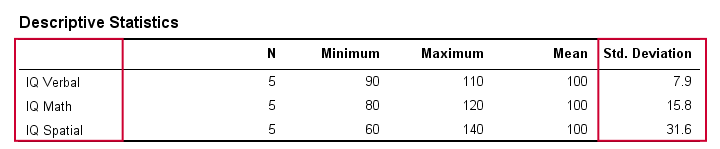
W prawdziwym życiu, oczywiście nie sprawdzamy wizualnie surowych wyników, aby zobaczyć jak daleko od siebie leżą. Zamiast tego, po prostu każemy oprogramowaniu obliczyć je dla nas (więcej na ten temat później). Poniższa tabela pokazuje odchylenia standardowe i kilka innych statystyk dla naszych danych IQ. Zauważ, że odchylenia standardowe potwierdzają wzór, który widzieliśmy w surowych danych.

Odchylenie standardowe i histogram

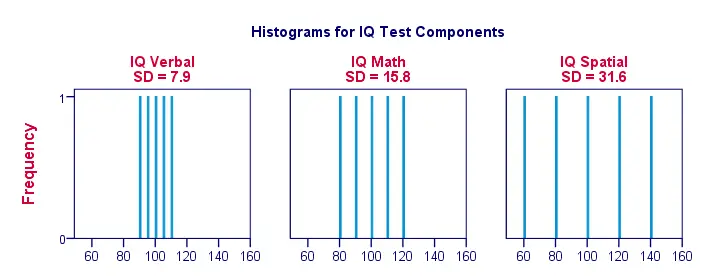
Dobrze, zróbmy rzeczy trochę bardziej wizualne. Poniższy rysunek pokazuje odchylenia standardowe i histogramy dla naszych wyników IQ. Zauważ, że każdy słupek reprezentuje wynik jednego kandydata w jednym elemencie IQ. Po raz kolejny widzimy, że odchylenia standardowe wskazują stopień, w jakim wyniki są od siebie oddalone.

Odchylenie standardowe – więcej histogramów

Gdy wizualizujemy dane tylko dla garstki obserwacji, jak na poprzednim rysunku, łatwo widzimy jasny obraz. Dla bardziej realistycznego przykładu, poniżej przedstawimy histogramy dla 1000 obserwacji. Co ważne, histogramy te mają identyczne skale; dla każdego histogramu, jeden centymetr na osi x odpowiada około 40 'punktom składowym IQ’.

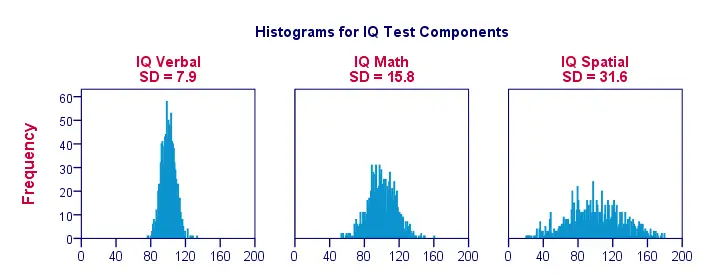
Zauważ, jak histogramy pozwalają na przybliżone oszacowanie odchyleń standardowych. Szersze” histogramy wskazują na większe odchylenia standardowe; wyniki (oś x) leżą dalej od siebie. Ponieważ wszystkie histogramy mają identyczną powierzchnię (odpowiadającą 1000 obserwacji), wyższe odchylenia standardowe są również związane z 'niższymi’ histogramami.

Odchylenie standardowe – Wzór na populację

Więc jak Twoje oprogramowanie oblicza odchylenia standardowe? Cóż, podstawowy wzór to

$$sigma = \sqrt{frac{suma(X – \mu)^2}{N}}$$

gdzie

• $(X) oznacza każdą oddzielną liczbę;
• (X) oznacza średnią ze wszystkich liczb, a
• (Xsum) oznacza sumę.

  Importantly, this formula assumes that your data contain the entire population of interest (hence „population formula”). Jeśli twoje dane zawierają tylko próbkę z populacji docelowej, zobacz poniżej.

  Formuła populacji – oprogramowanie

  Możesz użyć tej formuły w arkuszach Google, OpenOffice i Excel, wpisując =STDEVP(...) do komórki. Określ liczby, nad którymi chcesz odchylenie standardowe między nawiasami i naciśnij Enter. Poniższy rysunek ilustruje ideę.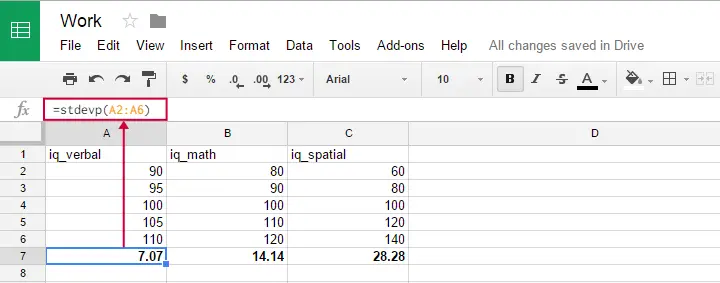

  

  Niestety, wydaje się, że wzór na odchylenie standardowe dla populacji nie istnieje w SPSS.

  Odchylenie standardowe – wzór na próbkę

  A teraz coś trudnego: jeśli Twoje dane są (w przybliżeniu) prostą próbką losową z jakiejś (znacznie) większej populacji, to poprzedni wzór będzie systematycznie zaniżał odchylenie standardowe w tej populacji. Bezstronny estymator odchylenia standardowego w populacji można uzyskać za pomocą

  $$S_x = \sqrt{ \frac{suma(X – \overline{X})^2}{N -1}}$$

  Jeśli chodzi o obliczenia, duża różnica w stosunku do pierwszego wzoru polega na tym, że dzielimy przez \(n -1}) zamiast przez \(n -1}). Dzieląc przez mniejszą liczbę otrzymujemy (nieco) większy wynik. Kompensuje to dokładnie wspomniane wcześniej niedoszacowanie. Jednak dla dużych liczebności próby oba wzory mają praktycznie identyczne wyniki.
  W GoogleSheets, Open Office i MS Excel, funkcja STDEV używa tego drugiego wzoru. Jest to również (jedyna) formuła odchylenia standardowego zaimplementowana w SPSS.

  Odchylenie standardowe i wariancja

  Drugą liczbą, która wyraża, jak daleko od siebie znajduje się zestaw liczb, jest wariancja. Wariancja jest kwadratem odchylenia standardowego. Oznacza to, że podobnie jak odchylenie standardowe, wariancja ma zarówno wzór na populację, jak i na próbkę.
  Zasadniczo niezręczne jest to, że dwie różne statystyki w zasadzie wyrażają tę samą własność zbioru liczb. Dlaczego po prostu nie odrzucimy wariancji na rzecz odchylenia standardowego (lub odwrotnie)? Podstawowa odpowiedź jest taka, że odchylenie standardowe ma bardziej pożądane właściwości w niektórych sytuacjach, a wariancja w innych.