Wprowadzenie :
Podobieństwo cosinusowe służy do określania podobieństwa między dokumentami lub wektorami. Matematycznie, mierzy cosinus kąta między dwoma wektorami rzutowanymi w przestrzeni wielowymiarowej. Istnieją inne techniki pomiaru podobieństwa, takie jak odległość euklidesowa lub odległość Manhattanu, ale będziemy skupiać się tutaj na podobieństwie cosinusowym i odległości cosinusowej.
Zależność między podobieństwem cosinusowym a odległością cosinusową można zdefiniować następująco.
- Podobieństwo maleje, gdy odległość między dwoma wektorami rośnie

2. Podobieństwo rośnie, gdy odległość między dwoma wektorami maleje.

Podobieństwo cosinusowe i odległość cosinusowa:
Podobieństwo cosinusowe mówi, że aby znaleźć podobieństwo między dwoma punktami lub wektorami, musimy znaleźć kąt między nimi.
Formuła na znalezienie podobieństwa cosinusowego i odległości jest jak poniżej:


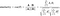
Tutaj A=Punkt P1,B=Punkt P2 (w naszym przykładzie)
Zobaczmy różne wartości Cos Θ aby zrozumieć podobieństwo cosinusowe i odległość cosinusową pomiędzy dwoma punktami danych (wektorami) P1 & P2 biorąc pod uwagę dwie osie X i Y.
Poniżej rysunek przedstawiający przypadki.
Przypadek 1: Gdy kąt między punktami P1 & P2 wynosi 45 stopni to
cosine_similarity= Cos 45 = 0.525
Przypadek 2: Gdy dwa punkty P1 & P2 są od siebie oddalone i kąt między punktami wynosi 90 Stopni to
cosine_similarity= Cos 90 = 0
Przypadek 3: Gdy dwa punkty P1 & P2 są bardzo blisko siebie i leżą względem siebie na tej samej osi, a kąt między nimi jest równy 0 stopni to
cosine_similarity= Cos 0 = 1

Poniżej rysunek przedstawiający kolejne trzy przypadki.
Przypadek 4: Gdy punkty P1 & P2 leżą naprzeciw siebie i kąt między nimi wynosi 180 stopni to
cosine_similarity= Cos 180 = -1
Przypadek 5: Gdy kąt między punktami P1 & P2 wynosi 270 stopni to
cosine_similarity= Cos 270 = 0
Przypadek 6: Gdy kąt między punktami P1 & P2 wynosi 360 Stopni wtedy
cosine_similarity= Cos 360 = 1

Przekażmy te wartości każdego z kątów omówionych powyżej i zobaczmy odległość cosinusową między dwoma punktami.
1 – Cosine_Similarity=Cosine_Distance
Case 1: When Cos 45 Degree
Lets replace the values in above formula .
1-0.525= Cosine_Distance
0.475 =Odległość cosinusowa
Przypadek 2: Gdy cos 90 stopni
1-0= Odległość cosinusowa
1 =Odległość cosinusowa
Przypadek 3: Gdy cos 0 stopni
1-1= Odległość cosinusowa
0 =Odległość cosinusowa
Przypadek 4: Gdy cos 180 stopni
1-(-1)=Cosinus
2 =Cosinus
Case 5: Gdy cos 270 stopni
1-0= Cosinus
1 =Cosinus
1 =Cosinus
Case 6: Kiedy Cos 360 Degree
1-1= Cosine_Distance
0 =Cosine_Distance
Widzimy wyraźnie, że kiedy odległość jest mniejsza, podobieństwo jest większe (punkty są blisko siebie), a odległość jest większa, dwa punkty są niepodobne (daleko od siebie)
Podobieństwo cosinusowe i odległość cosinusowa są mocno wykorzystywane w systemach rekomendacji do polecania produktów użytkownikom na podstawie ich upodobań.
Kilka przykładów gdzie jest to używane to strony internetowe takie jak Amazon,Flipkart aby polecać produkty klientom dla spersonalizowanego doświadczenia,Oceny filmów i rekomendacji itp.
Zakończenie: Mam nadzieję, że do tej pory masz jasne zrozumienie matematyki za obliczeniem podobieństwa cosinusowego i odległości cosinusowej i jego wykorzystania.
Mam nadzieję, że podoba Ci się mój artykuł.Proszę uderzyć Clap 👏(50 razy), aby zmotywować mnie do pisania dalej.
Chcesz się połączyć :
Linked In : https://www.linkedin.com/in/anjani-kumar-9b969a39/
Jeśli podobają Ci się moje posty tutaj na Medium i chciałbyś, abym dalej wykonywał tę pracę, rozważ wsparcie mnie na patreon
.
