Szacowanie trójpunktowe i rozkład PERT (szacowanie kosztów i czasu)

Oszacowanie czasu, wysiłku i kosztów jest jedną z najbardziej krytycznych części zarządzania projektami. Wynika to z fundamentalnego znaczenia tych szacunków dla całego procesu planowania projektu, a w szczególności dla określenia zakresu, harmonogramu i poziomu bazowego kosztów. Jedną z technik estymacji sugerowanych w podręczniku PMI Project Management Body of Knowledge (PMBOK 6th ed., rozdz. 6.4, 7.2) jest estymacja trzypunktowa stosowana z rozkładem trójkątnym, Beta lub PERT. W tym artykule przedstawimy te metody.

Czym jest technika estymacji trzypunktowej?

Eliminacja trzypunktowa jest prostym, ale użytecznym podejściem do szacowania czasu lub kosztu elementów pracy. Zgodnie z metodologią PMI, jest ona stosowana w grupach procesów „Szacowanie czasu trwania działań” i „Szacowanie kosztów”. Technika ta obejmuje trzy różne szacunki, które są zwykle uzyskiwane od ekspertów przedmiotowych:

• Optymistyczny szacunek,
• Pesymistyczny szacunek,
• Najbardziej prawdopodobny szacunek.

Oszacowanie optymistyczne to oczekiwana ilość pracy lub czasu potrzebna do wykonania czynności przy założeniu, że nie występują żadne przeszkody i wszystko przebiega bezproblemowo. Reprezentuje on tak zwany najlepszy scenariusz. Punkt pesymistyczny opiera się na założeniu, że było odwrotnie – reprezentuje najgorszy scenariusz. Chociaż oba szacunki odnoszą się do skrajnych punktów zakresu oczekiwanych wyników, szacunki te mają być w pewnym stopniu realistyczne.

Trzeci punkt odzwierciedla najbardziej prawdopodobny przypadek, jest to szacunek pracy lub czasu, który jest uważany za najbardziej realistyczny. Można ulec pokusie, aby po prostu użyć średniej pomiędzy punktami optymistycznym i pesymistycznym bez zastanowienia. Jednak w wielu przypadkach może to nie być właściwe. W praktyce, zazwyczaj warto prawidłowo określić ten najbardziej prawdopodobny szacunek, analogicznie do innych punktów szacowania.

Wynikiem trzypunktowego szacowania jest tak zwany trójkątny rozkład wartości czasu lub kwot kosztów, składający się z trzech szacunków (patrz ilustracja poniżej).

Czym jest PERT?

PERT oznacza Program Evaluation and Review Technique i został opracowany jako zaawansowany system planowania i zarządzania harmonogramem projektu przez marynarkę wojenną Stanów Zjednoczonych w latach pięćdziesiątych (źródło: Heldman, PMP Study guide, rozdz. 4).

Inna, niezbyt poważna, historia jego powstania została kiedyś opublikowana przez anonimowego autora w czasopiśmie PMI (Link; źródło: Anonymous (1975). PERT-the hoax of the century. Project Management Quarterly, 6(3), 22-23).

W projektach w stylu PMI, PERT jest przede wszystkim wykorzystywany jako technika uzupełniająca do Metody Ścieżki Krytycznej przy planowaniu działań. Jednakże, może być również stosowany do samodzielnego szacowania pozycji pracy i działań.

Tzw. rozkład PERT wykorzystuje wartości określone za pomocą techniki szacowania trzypunktowego. W zasadzie może być stosowany na wszystkich poziomach planowania, od działań do całych projektów. Jednak znalezienie odpowiedniej ziarnistości dla znaczącego szacowania może wymagać pewnego krytycznego i koncepcyjnego myślenia.

Metoda PERT zakłada przeważenie „najbardziej prawdopodobnego” oszacowania. Przekształca ona trzypunktową estymatę w krzywą w kształcie dzwonu i pozwala określić prawdopodobieństwa zakresów wartości oczekiwanych.

Jakie są różnice między rozkładem trójkątnym a rozkładem PERT estymat trzypunktowych?

Podczas gdy rozkład trójkątny uwzględnia tylko trzy estymowane punkty, metoda PERT pozwala przekształcić trzypunktową estymatę w krzywą w kształcie dzwonu, o prawie normalnym rozkładzie, dzięki czemu można ją wykorzystać do obliczenia prawdopodobieństw zakresów wartości oczekiwanych.

Następujący diagram ilustruje różnice między rozkładem PERT, rozkładem trójkątnym i przedstawieniem estymaty trzypunktowej jako rozkładu normalnego.

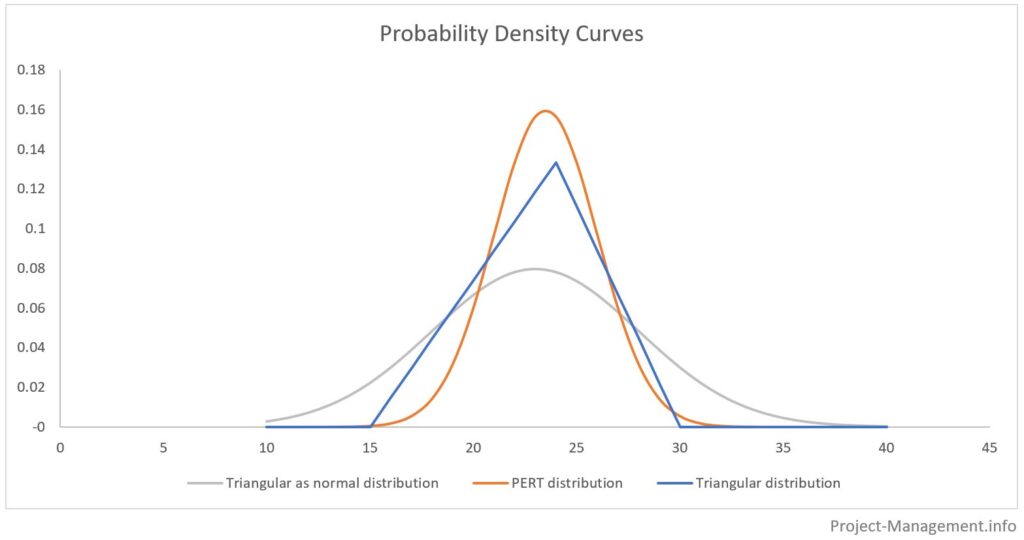
Obszary pod krzywymi rozkładu prawdopodobieństwa reprezentują skumulowane prawdopodobieństwa odpowiednich przedziałów estymacji. Zazwyczaj zakresy te są wyznaczane za pomocą wartości oczekiwanej +/- odchylenie standardowe pomnożone przez 1, 2 i 3. Ilustruje to poniższy rysunek:

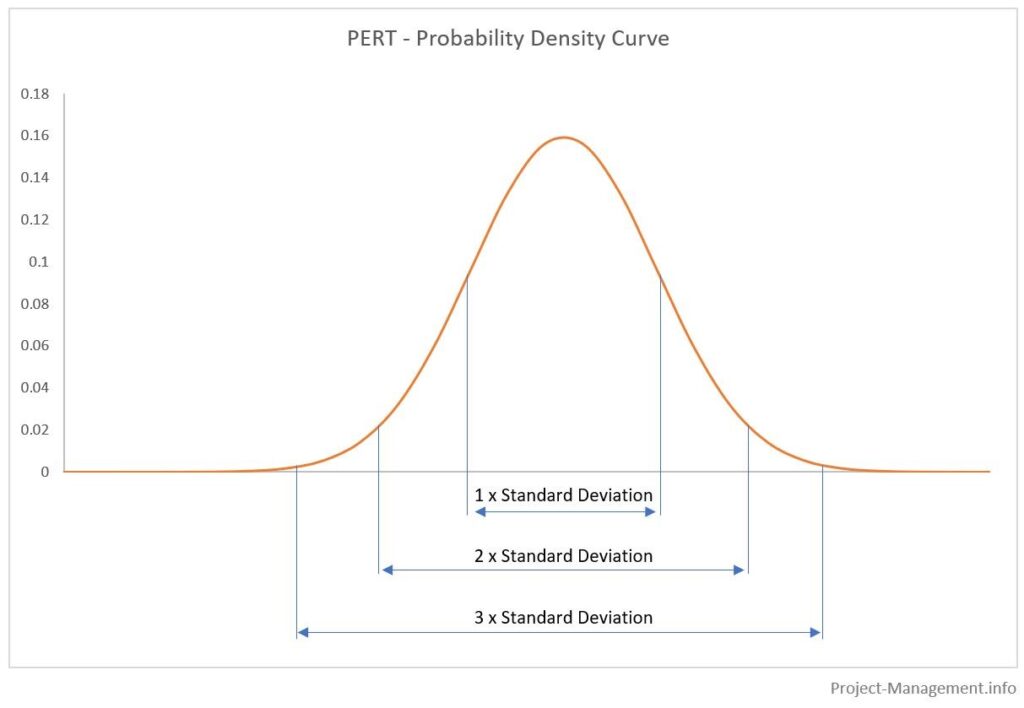
Wynikowe prawdopodobieństwa (w przybliżeniu) wynoszą

• 68,3% dla 1 odchylenia standardowego,
• 95.5% dla 2 odchyleń standardowych,
• 99,7% dla 3 odchyleń standardowych.

Wiedza wymagana na egzaminie PMP ogranicza się do obliczania oczekiwanych oszacowań i znajomości różnych prawdopodobieństw (źródło). Dlatego w tym artykule nie będziemy zajmować się szczegółami statystycznymi i tłem – można je znaleźć na Riskamp.

Użyj tego kalkulatora do wyznaczenia trzypunktowych wartości szacunkowych i PERT.

How Is Three-Point Estimate Calculated?

The Triangular Distribution

Proste, ale powszechnie stosowane obliczenie involvesthe average lub mean of the 3 estimated values. Wzór rozkładu trójkątnego to:

E =(O + M + P) / 3

gdzie:
E = Oczekiwana ilość czasu lub kosztów,
O = Optymistyczne oszacowanie,
M = Najbardziej prawdopodobne oszacowanie,
P = Pesymistyczne oszacowanie.

Waga każdego oszacowania w tym równaniu jest identyczna. Zatem przypadek „najbardziej prawdopodobny” nie wpływa na ostateczne oszacowanie bardziej niż 2 mniej prawdopodobne oszacowania. Różni się to od metody rozkładu beta.

Rozkład beta PERT

Rozkład beta PERT uwzględnia fakt, że wystąpienie przypadku „najbardziej prawdopodobnego” jest bardziej prawdopodobne, co jest odzwierciedlone w mnożniku dla tego oszacowania. Metodologia PMI sugeruje to obliczenie jako alternatywę dla rozkładu trójkątnego dla oszacowań kosztów (jesteśmy jednak zdania, że może być ono również stosowane do oszacowań czasu).

W tej metodzie najbardziej prawdopodobne oszacowanie otrzymuje mnożnik 4, podczas gdy ogólny dzielnik jest zwiększony do 6. Wzór jest następujący:

E =(O + 4*M + P) / 6

gdzie:
E = Oczekiwana ilość czasu lub koszt,
O = Szacunek optymistyczny,
M = Szacunek najbardziej prawdopodobny,
P = Szacunek pesymistyczny.

Odchylenie standardowe rozkładu PERT jest obliczane za pomocą wzoru:

Odchylenie standardowe = (P – O) / 6

W przypadku szacowania całej ścieżki (analogiczna metoda ścieżki krytycznej) stosowana jest podobna koncepcja, jednak z wykorzystaniem łącznego odchylenia standardowego wszystkich działań.

Przykład szacowania trzypunktowego i PERT

Zespół ekspertów przedmiotowych szacuje czas potrzebny do wykonania czynności. W tym przykładzie czas trwania czynności jest szacowany przy użyciu techniki szacowania trzypunktowego.Otrzymują oni następujące liczby:

.

Szacunek optymistyczny	15 dni
Szacunek pesymistyczny	24 dni
Najbardziej prawdopodobny szacunek	30 dni

Wartości wahają się od 15 dni (optymistyczne) do 30 dni (pesymistyczne). Czas trwania wynoszący 24 dni jest uważany za najbardziej prawdopodobną ilość czasu potrzebną do ukończenia pracy.

Obliczanie oczekiwanego czasu trwania przy użyciu rozkładu trójkątnego

Przewidywany czas trwania przy użyciu rozkładu trójkątnego oblicza się w następujący sposób:

FinalEstimate = (15 + 30 + 24) / 3.

Wynikowy ostateczny szacunek w tej metodzie wynosi 23, co jest w zasadzie nieważoną średnią z 3 szacunków.

Obliczanie oczekiwanego czasu trwania przy użyciu rozkładu beta PERT

Przewidywany czas trwania można również obliczyć przy użyciu metody PERT:

FinalEstimate (wartość oczekiwana) = (15 + 4×24 + 30) / 6.

Wynikowa wartość oczekiwana wynosi 23,5 dnia, co jest większe niż ostateczna wartość szacunkowa określona przy użyciu metody trójkątów. Wynika to z wyższej wagi (tj. mnożnika 4), która jest przypisana do estymacji „najbardziej prawdopodobnej”.

Odchylenie standardowe tej estymacji wynosi:

StandardDeviation = (30 – 15) / 6 = 2,5

Determining the Probabilities of the Expected Duration

Obliczenie oczekiwanego czasu trwania oraz odchylenia standardowego umożliwia kierownikowi projektu określenie prawdopodobieństwa (ok.):

Zakres	Prawdopodobieństwo	Dolna granica	Górna granica
1 x odchylenie standardowe	68.3%	21	26
2 x odchylenie standardowe	95.5%	18,5	28,5
3 x odchylenie standardowe	99.7%	16	31

Z prawdopodobieństwem 68,3% czas trwania aktywności wyniesie od 21 do 26 dni. Dla przedziału od 18,5 do 28,5 dni prawdopodobieństwo wynosi 95,5%. Użycie 3 odchyleń standardowych obejmuje prawie wszystkie punkty danych i określa 99,7% prawdopodobieństwo, że czas trwania będzie ostatecznie wynosił od 16 do 31 dni.

Podsumowanie

Ocena końcowa w metodzie trójkątów wyniosła 23, w porównaniu z 23,5 przy użyciu metody PERT. Wynika to z faktu, że metoda ta przypisuje wyższą wagę „najbardziej prawdopodobnemu” przypadkowi, który w naszym przypadku nie jest dokładnie średnią (lub średnią nieważoną) optymistycznego i pesymistycznego oszacowania.

Użycie metody PERT pozwala na uwzględnienie prawdopodobieństw zakresów wartości. Jest to przydatne, gdy jakość oszacowań jest różna, np. gdy różnica między oszacowaniami optymistycznymi i pesymistycznymi znacznie odbiega od siebie w różnych działaniach. W takim przypadku użycie zakresów i ich prawdopodobieństw odzwierciedli rozproszenie i poziom pewności szacunków bazowych.

Podsumowanie

Oszacowanie działań w odniesieniu do ich wymagań czasowych i kosztowych jest kluczowe dla planowania i harmonogramowania projektów i działań. W wielu projektach dokładniejsze szacunki, takie jak szacunki parametryczne, oparte na przykład na korelacjach statystycznych porównywalnych projektów z przeszłości, nie są dostępne. Technika szacowania trzypunktowego oferuje dobre podejście do przetwarzania i równoważenia szacunków odgórnych lub szacunków ekspertów przedmiotowych w takich sytuacjach.

Rozkład PERT jest prawdopodobnie najbardziej dokładną metodą agregowania tych najgorszych, najlepszych i najbardziej prawdopodobnych przypadków w pojedynczą liczbę (wartość oczekiwaną) lub zakres wartości. Dzięki zastosowaniu odchylenia standardowego, uwzględnia on zarówno nieodłączną niepewność, jak i potencjalny rozrzut oszacowań.

To może być powód, dla którego PERT jest nadal powszechnie stosowaną metodą w szacowaniu i harmonogramowaniu projektów, mimo że istnieje już od kilku dziesięcioleci i mogli z niej korzystać już nasi dziadkowie (gdyby byli kierownikami projektów).

.