Zastosowanie twierdzenia Buckinghama Pi

Następne: Importance of Non-Dimensional Numbers Up: Buckingham Pi Theorem Previous: Buckingham Pi Theorem

Application of Buckingham Pi theorem

Podane przez nas twierdzenie jest bardzo ogólne, ale w żaden sposób nie ogranicza się do mechaniki płynów. Jest ono używane w różnych dziedzinach, takich jak botanika i nauki społeczne, a książki i tomy zostały napisane na ten temat. Nie potrzebujemy jednak zbyt wiele teorii, aby móc ją zastosować. To, co rozważymy, to procedura wykorzystania twierdzenia i uzyskania liczb niewymiarowych dla danego przepływu.

1. Wymień wszystkie zmienne, które rządzą procesem. Zmienne te powinny być niezależne od siebie. Na przykład, nie należy wybierać gęstości, ciężaru i ciężaru właściwego. Gęstość i ciężar właściwy powinny wystarczyć. Dla naszego problemu mamy F, D, V, i . Mamy n = 5.
2. Zaznacz zmienne powtarzające się. W naszym przypadku są to D, V i co daje k = 3 .
3. Zdecyduj ile jest liczb niewymiarowych. Dla naszego przypadku mamy n – k = 2. Nasz problem ma 2 liczby niewymiarowe, i .
4. Zdefiniuj liczby niewymiarowe grupując zmienne w n – k grup tak, aby każda grupa miała wszystkie zmienne powtarzające się i jedną zmienną nie powtarzającą się. Zatem dla naszego problemu mamy

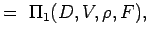
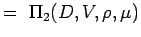
   		(5.2)
   Let
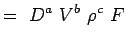
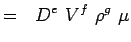
   		(5.3)

5. Teraz wyrażmy każdą zmienną w kategoriach jej wymiarów. Zastosujmy system MLT, zgodnie z którym zmienne dla naszych problemów mają następujące wymiary.
   

   Zmienna	Wymiary
   F, Siła	M L / T2 lub M L T-2
   D, Średnica:	L
   V, Velocity	L/T lub LT-1
   , Gęstość:	M/L3 lub ML-3
   , Lepkość	ML-1T-1

   Substituting these dimensions into Eqn. 5.2, mamy

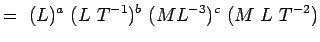
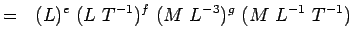
   		(5.4)
   Or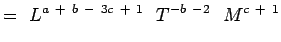
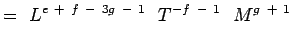
   		(5.5)

   Zauważając, że i są niewymiarowe mamy,

   a + b – 3c + 1 = 0; -b – 2 = 0, c + 1 = 0
   e + f – 3g – 1 = 0; -f – 1 = 0;g + 1 = 0	(5.6)

   Rozwiązanie równań daje,

   a = -2, b = -2, c = -1
   e = -1, f = -1, g = -1	(5.7)

   Teraz nasze liczby niewymierne stają się,

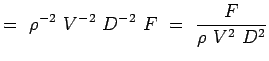
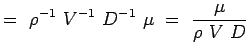
   		(5.8)

W ten sposób znaleźliśmy liczby niewymiarowe dla interesującego nas przepływu, a mianowicie oporu wokół cylindra kołowego. Zależność funkcyjna pomiędzy tymi dwiema liczbami może być wyrażona jako

Zauważmy jednak, że postać wyrażenia , które wyprowadziliśmy jest nieco inna od tej, którą przyjęliśmy na początku. Prawa strona równania jest w rzeczywistości odwrotnością liczby Reynoldsa! Wskazuje to na wadę analizy, że nie można uzyskać dokładnej postaci funkcyjnej pomiędzy liczbami . Jakikolwiek uzyskany współczynnik lub indeks nie może być określony na podstawie tej analizy. To powinno być ustalone przez eksperymenty lub przez obliczenia. Ale ponieważ liczby są niewymiarowe możemy canalways napisać,

Następnie: Importance of Non-Dimensional Numbers Up: Buckingham Pi Theorem Previous: Buckingham Pi Theorem

(c) Aerospace, Mechanical & Mechatronic Engg. 2005
University of Sydney
.