Aplicarea teoremei lui Buckingham Pi

Continuare: Importanța numerelor adimensionale Up: Teorema lui Buckingham Pi Previous: Teorema lui Buckingham Pi

Aplicația teoremei lui Buckingham Pi

Teorema pe care am enunțat-o este una foarte generală, dar nicidecum limitată la mecanica fluidelor. Ea este utilizată în domenii diversificate, cum ar fi Botanica și Științele sociale și s-au scris cărți și volume pe această temă. Dar nu avem nevoie de multă teorie pentru a o putea aplica. Ceea ce vom lua în considerare este o procedură de utilizare a teoremei și de obținere a numerelor nedimensionale pentru un flux dat.

1. Enumerați toate variabilele care guvernează procesul. Aceste variabile trebuie să fie independente unele de altele. De exemplu, nu ar trebui să se aleagă densitatea, gravitația și greutatea specifică. Densitatea și greutatea specifică ar trebui să fie suficiente. Pentru problema noastră avem F, D, V, și . Avem n = 5.
2. Marcați variabilele care se repetă. În cazul nostru acestea sunt D, V și , ceea ce face k = 3 .
3. Decideți câte numere non-dimensionale există. Pentru cazul nostru avem n – k = 2. Problema noastră are 2 numere nedimensionale, și .
4. Definiți numerele nedimensionale prin gruparea variabilelor în n – k grupuri astfel încât fiecare grup să aibă toate variabilele repetitive și o variabilă nerepetitivă. Astfel, pentru problema noastră avem

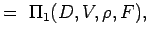
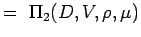
   		(5.2)
   Let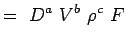
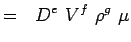
   		(5.3)

5. Exprimăm acum fiecare variabilă în funcție de dimensiunile sale. Să folosim sistemul MLT conform căruia variabilele pentruproblemele noastre au următoarele dimensiuni.
   

   	Variabilă	Dimensiuni
   F, Forța	M L / T2 sau M L T-2
   D, Diametrul:	L
   V, Viteză	L/T sau LT-1
   , Densitate:
   , Densitate:	M/L3 sau ML-3
   , Vâscozitatea	ML-1T-1

   Substituind aceste dimensiuni în ecuația:

   . 5.2, avem

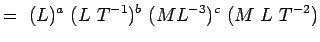
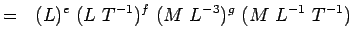
   		(5.4)
   Or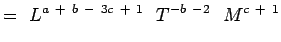
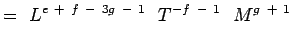
   		(5.5)

   Notând că și sunt nedimensionale avem,

   	a + b – 3c + 1 = 0; -b – 2 = 0, c + 1 = 0
   e + f – 3g – 1 = 0; -f – 1 = 0;g + 1 = 0	(5.6)

   Soluționând ecuațiile se obține,

   a = -2, b = -2, c = -1
   e = -1, f = -1, g = -1	(5.7)

   Acum, numerele noastre non-dimensionale devin,

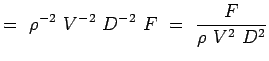
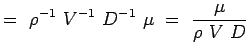
   		(5.8)

Acum am găsit numerele adimensionale pentru curgerea de interes, și anume, rezistența în jurul unui cilindru circular. Relația funcțională dintre cele două numere poate fi exprimată ca

Dar rețineți că forma termenului pe care am derivat-o este oarecumdiferită de cea pe care am presupus-o la început. Partea dreaptă a ecuației este, de fapt, inversul numărului lui Reynolds!Acest lucru indică dezavantajul analizei că nu se poate obține forma exactăfuncțională dintre numerele . Oricecoeficient sau indice obținut nu poate fi determinat prin această analiză. Acesta ar trebui să fie determinat prin experiment sau prin calcul. Dar din moment ce numerele sunt nedimensionale, putem să scriem,

Continuare: Importanța numerelor nedimensionale Up: Teorema lui Buckingham Pi Previous: Teorema lui Buckingham Pi

(c) Aerospace, Mechanical & Mechatronic Engg. 2005
Universitatea din Sydney
.