O deviație standard este un număr care ne spune
în ce măsură un set de numere se află la distanță.O deviație standard poate varia de la 0 la infinit. O abatere standard de 0 înseamnă că o listă de numere sunt toate egale -nu se distanțează deloc.
Ecart standard – Exemplu
Cinci candidați au făcut un test IQ ca parte a unei cereri de angajare. Scorurile lor la cele trei componente ale IQ-ului sunt prezentate mai jos.
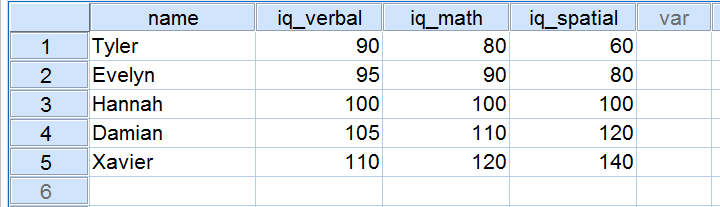
Acum, să analizăm cu atenție scorurile la cele 3 componente ale IQ-ului. Observați că toate trei au o medie de 100 pe cei 5 candidați ai noștri. Cu toate acestea, scorurile la iq_verbal se află mai aproape unul de celălalt decât scorurile la iq_math. În plus, scorurile la iq_spatial sunt mai îndepărtate decât scorurile la primele două componente. Măsura exactă în care un număr de scoruri se distanțează poate fi exprimată sub forma unui număr. Acest număr este cunoscut sub numele de deviație standard.
Deviație standard – Rezultate
În viața reală, în mod evident, nu inspectăm vizual scorurile brute pentru a vedea cât de mult se distanțează între ele. În schimb, vom cere pur și simplu unui software să le calculeze pentru noi (mai multe despre asta mai târziu). Tabelul de mai jos prezintă abaterile standard și alte câteva statistici pentru datele noastre de IQ. Observați că abaterile standard confirmă tiparul pe care l-am văzut în datele brute.
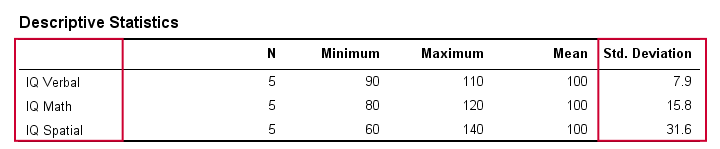
Ecart standard și histogramă
În regulă, să facem lucrurile un pic mai vizuale. Figura de mai jos arată deviațiile standard și histogramele pentru scorurile noastre IQ. Rețineți că fiecare bară reprezintă scorul unui candidat la o componentă IQ. Încă o dată, observăm că abaterile standard indică măsura în care scorurile se distanțează între ele.
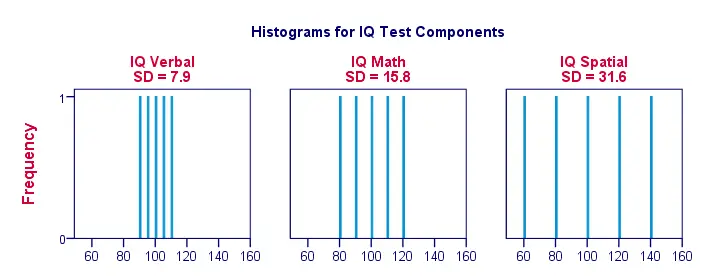
Ecart standard – Mai multe histograme
Când vizualizăm datele privind doar o mână de observații, ca în figura anterioară, vedem cu ușurință o imagine clară. Pentru un exemplu mai realist, vom prezenta mai jos histograme pentru 1.000 de observații. Este important faptul că aceste histograme au scări identice; pentru fiecare histogramă, un centimetru pe axa x corespunde la aproximativ 40 de „puncte ale componentei IQ”.
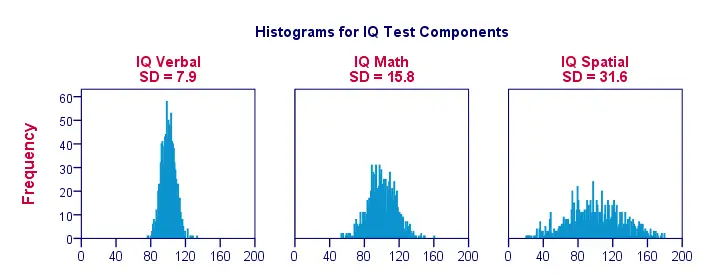
Rețineți cum histogramele permit estimări aproximative ale deviațiilor standard. Histogramele ‘mai largi’ indică abateri standard mai mari; scorurile (axa x) se află la distanțe mai mari. Deoarece toate histogramele au suprafețe identice (corespunzătoare la 1.000 de observații), abaterile standard mai mari sunt, de asemenea, asociate cu histograme ‘mai mici’.
Ecart standard – Formula populației
Atunci cum calculează softul dumneavoastră abaterile standard? Ei bine, formula de bază este
$$\sigma = \sqrt{\frac{\sum(X – \mu)^2}{N}}$$$
unde
- \(X\) denumește fiecare număr separat;
- \(\mu\) desemnează media tuturor numerelor și
- \(\sum\) desemnează o sumă.
Cu alte cuvinte, abaterea standard este rădăcina pătrată a diferenței medii pătratice dintre fiecare număr individual și media acestor numere.
Important este faptul că această formulă presupune că datele dvs. conțin întreaga populație de interes (de aici „formula populației”). Dacă datele dvs. conțin doar un eșantion din populația țintă, vedeți mai jos.
Formula de populație – Software
Puteți utiliza această formulă în Google sheets, OpenOffice și Excel prin tastarea =STDEVP(...) într-o celulă. Specificați numerele peste care doriți abaterea standard între paranteze și apăsați Enter. Figura de mai jos ilustrează ideea.
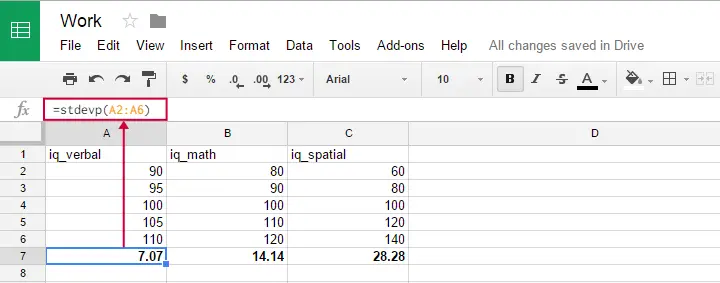
În mod ciudat, formula abaterii standard a populației nu pare să existe în SPSS.
Standard Deviation – Sample Formula
Acum pentru ceva provocator: dacă datele dvs. sunt (aproximativ) un simplu eșantion aleatoriu dintr-o anumită populație (mult) mai mare, atunci formula anterioară va subestima sistematic abaterea standard în această populație. Un estimator nepărtinitor pentru abaterea standard a populației se obține folosind
$$S_x = \sqrt{\frac{\sum(X – \overline{X})^2}{N -1}}$$
În ceea ce privește calculele, marea diferență față de prima formulă este că împărțim prin \(n -1\) în loc de \(n\). Împărțind la un număr mai mic rezultă un rezultat (ușor) mai mare. Acest lucru compensează exact subestimarea menționată mai sus. Cu toate acestea, pentru eșantioane de dimensiuni mari, cele două formule au rezultate practic identice.
În GoogleSheets, Open Office și MS Excel, funcția STDEV utilizează această a doua formulă. Este, de asemenea, (singura) formulă de deviație standard implementată în SPSS.
Deviație standard și varianță
Un al doilea număr care exprimă cât de departe se află un set de numere este varianța. Varianța este abaterea standard la pătrat. Acest lucru implică faptul că, în mod similar abaterii standard, varianța are o formulă de populație, precum și o formulă de eșantion.
În principiu, este ciudat ca două statistici diferite să exprime practic aceeași proprietate a unui set de numere. De ce să nu eliminăm pur și simplu varianța în favoarea abaterii standard (sau invers)? Răspunsul de bază este că abaterea standard are proprietăți mai dezirabile în anumite situații, iar varianța în altele.
.
