Estimarea timpului, a eforturilor și a costurilor este una dintre cele mai importante părți ale managementului de proiect. Acest lucru se datorează importanței fundamentale a acestor estimări pentru întreaga planificare a proiectului și, în special, pentru linia de bază a domeniului de aplicare, a calendarului și a costurilor. Una dintre tehnicile de estimare sugerate în PMI Project Management Body of Knowledge (PMBOK ed. a 6-a, cap. 6.4, 7.2) este estimarea în trei puncte utilizată cu distribuția triunghiulară, Beta sau PERT. Vom prezenta aceste metode în acest articol.
Ce este tehnica de estimare în trei puncte?
Stimarea în trei puncte este o abordare simplă, dar utilă, pentru a estima timpul sau costul elementelor de lucru. Conform metodologiei PMI, este utilizată în grupurile de procese „Estimarea duratei activității” și „Estimarea costurilor”. Tehnica implică trei estimări diferite care sunt de obicei obținute de la experți în domeniu:
- Stimare optimistă,
- Stimare pesimistă,
- Stimare cea mai probabilă.
Stimarea optimistă este cantitatea de muncă sau timpul preconizat necesar pentru a efectua o activitate presupunând că nu apar impedimente și că totul decurge fără probleme. Ea reprezintă așa-numitul scenariu optimist. Punctul pesimist se bazează pe ipoteza că ar fi adevărat contrariul – reprezintă cel mai rău scenariu. Deși ambele estimări se referă la punctele extreme ale intervalului de rezultate așteptate, se presupune că estimările sunt oarecum realiste.
Cel de-al treilea punct reflectă cazul cel mai probabil, este estimarea muncii sau a timpului care este considerată a fi cea mai realistă. Cineva ar putea fi tentat să folosească pur și simplu media dintre punctele optimist și pesimist fără să se gândească mai mult. Cu toate acestea, este posibil ca acest lucru să nu fie adecvat pentru multe cazuri. În practică, în mod normal, merită să se determine în mod corespunzător această estimare cea mai probabilă, prin analogie cu celelalte puncte de estimare.
Rezultatul estimării în trei puncte este așa-numita distribuție triunghiulară a valorilor timpului sau a sumelor de cost, care cuprinde cele trei estimări (a se vedea ilustrația de mai jos).
Ce este PERT?
PERT este acronimul de la Program Evaluation and Review Technique (Tehnica de evaluare și revizuire a programului) și a fost dezvoltat ca un sistem avansat de planificare și management al planificării și managementului calendaristic al proiectelor de către marina americană în anii 1950 (sursa: Heldman, PMP Study guide, cap. 4).
O altă poveste, nu prea serioasă, despre originea sa a fost publicată cândva de un autor anonim în revista PMI (Link; sursa: Anonim (1975). PERT-the hoax of the century. Project Management Quarterly, 6(3), 22-23).
În proiectele de tip PMI, PERT este utilizat în primul rând ca o tehnică suplimentară la metoda căii critice pentru planificarea activităților. Cu toate acestea, poate fi, de asemenea, aplicată la estimări de sine stătătoare ale elementelor de lucru și activităților.
Așa-numita distribuție PERT se bazează pe valorile determinate cu tehnica de estimare în trei puncte. Ea poate fi utilizată în principiu pentru toate nivelurile de planificare, de la activități la proiecte întregi. Cu toate acestea, găsirea granularității potrivite pentru o estimare semnificativă poate necesita o anumită gândire critică și conceptuală.
Metoda PERT implică supraponderarea estimării „celei mai probabile”. Ea transformă estimarea în trei puncte într-o curbă în formă de clopot și permite determinarea probabilităților intervalelor de valori așteptate.
Care sunt diferențele dintre distribuția triunghiulară și PERTDistribuția estimărilor în trei puncte?
În timp ce distribuția triunghiulară ia în considerare doar cele trei puncte estimate, metoda PERT permite transformarea estimării în trei puncte într-o curbă în formă de clopot, distribuită aproape normal.Astfel, ea poate fi utilizată pentru calcularea probabilităților intervalelor de valori așteptate.
Graficul următor ilustreazădiferențele dintre distribuția PERT, distribuția triunghiulară și prezentarea estimării în trei puncte ca și cum ar fi o distribuție normală.
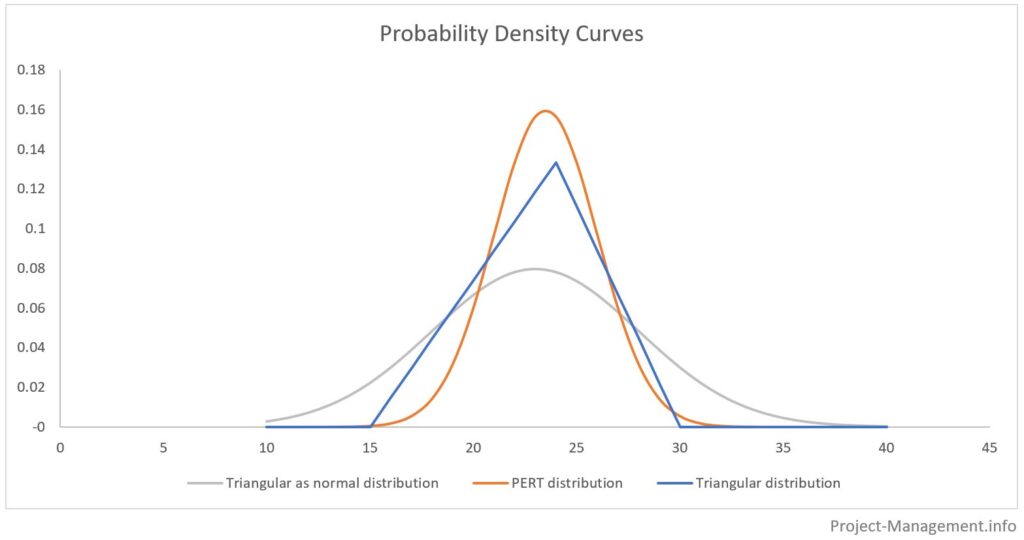
Ariile de sub curbele de distribuție a probabilităților reprezintă probabilitățile cumulate ale intervalelor respective de estimări. În mod obișnuit, aceste intervale sunt determinate cu valoarea așteptată +/- abaterea standard înmulțită cu 1, 2 și 3. Acest lucru este ilustrat în figura următoare:
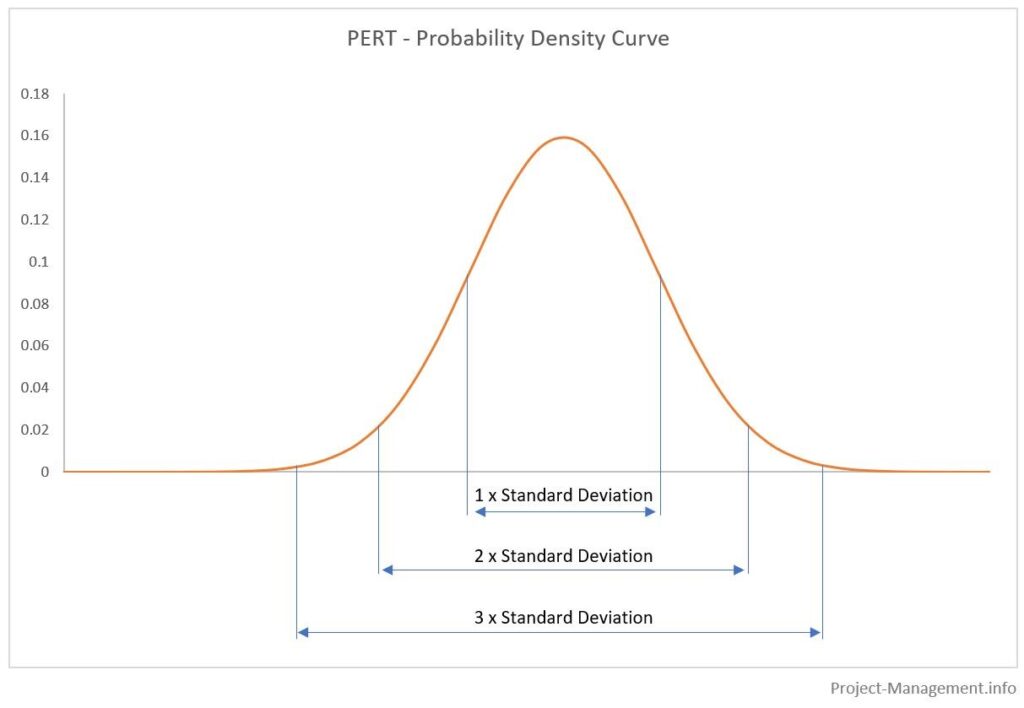
Probabilitățile rezultate (aproximativ) sunt
- 68,3% pentru 1 abatere standard,
- 95.5% pentru 2 abateri standard,
- 99,7% pentru 3 abateri standard.
Cunoștințele necesare pentru examenul PMP se limitează la calcularea estimărilor așteptate și la cunoașterea diferitelor probabilități (sursa). Prin urmare, nu vom acoperi detaliile statistice și contextul în acest articol – puteți găsi aceste detalii pe Riskamp.
Utilizați acest calculator pentru a determina estimările în trei puncte și PERT.
Cum se calculează estimarea în trei puncte?
Distribuția triunghiulară
Calculul simplu, dar utilizat în mod obișnuit, implică media sau media celor 3 valori estimate. Formula acestei distribuții triunghiulare este:
E =(O + M + P) / 3
în care:
E = Cantitatea de timp sau costul așteptat,
O = Estimarea optimistă,
M = Estimarea cea mai probabilă,
P = Estimarea pesimistă.
Primul PMBOK folosește t(E), t(O), t(M) și t(P) ca variabile pentru estimările de timp și c(E), c(O), c(M) și c(P).
Ponderea fiecărei estimări din această ecuație este identică. Astfel, cazul „cel mai probabil” nu afectează estimarea finală mai mult decât cele 2 estimări mai puțin probabile. Acest lucru este diferit de metoda distribuției beta.
Distribuția beta PERT
Distribuția beta PERT ia în considerare faptul că cazul „cel mai probabil” are o probabilitate mai mare de apariție, ceea ce se reflectă într-un multiplicator pentru acea estimare. Metodologia PMI sugerează acest calcul ca o alternativă la distribuția triunghiulară pentru estimările de costuri (cu toate acestea, suntem de părere că poate fi utilizată și pentru estimările de timp).
În această metodă, estimarea cea mai probabilă primește un multiplicator de 4, în timp ce divizorul general este mărit la 6. Formula este următoarea:
E =(O + 4*M + P) / 6
unde:
E = Cantitatea de timp sau costul așteptat,
O = Estimarea optimistă,
M = Estimarea cea mai probabilă,
P = Estimarea pesimistă.
Deviația standard a distribuției PERT se calculează cu ajutorul formulei:
Deviația standard = (P – O) / 6
Pentru estimarea unei întregi căi (metoda analogică a căii critice), se aplică un concept similar, folosind însă o deviație standard combinată a tuturor activităților.
Exemplu de estimare în trei puncte și PERT
O echipă de experți în domeniu estimează timpul necesar pentru finalizarea unei activități. În acest exemplu, durata unei activități este estimată cu ajutorul tehnicii de estimare în trei puncte.Ei ajung la următoarele cifre:
| Estimare optimistă | 15 zile |
| Estimare pesimistă | 24 zile |
| Estimarea cea mai probabilă | 30 de zile |
Valorile variază de la 15 zile (optimist)la 30 de zile (pesimist). O durată de 24 de zile este considerată a fi cea mai probabilă durată de timp necesară pentru finalizarea lucrării.
Calcularea duratei așteptate cu o distribuție triunghiulară
Durata așteptată folosind o distribuție triunghiulară se calculează după cum urmează:
Stimarea finală = (15 + 30 + 24) / 3.
Stimarea finală rezultată prin această metodă este 23, care este practic media neponderată a celor 3 estimări.
Calcularea duratei așteptate folosind distribuția PERT Beta
Durata așteptată poate fi calculată și prin metoda PERT:
Stimarea finală (valoarea așteptată) = (15 + 4×24 + 30) / 6.
Valoarea așteptată rezultată este de 23,5 zile, care este mai mare decât estimarea finală determinată prin metoda triunghiulară. Acest lucru se datorează ponderii mai mari (adică multiplicatorului de 4) care este atribuită estimării „cele mai probabile”.
Deviația standard a acestei estimări este:
Deviația standard = (30 – 15) / 6 = 2,5
Determinarea probabilităților duratei așteptate
Având calculat durata așteptată și deviația standard, managerul de proiect poate determina probabilitățile (aprox.):
| Interval | Probabilitate | Limita inferioară | Limita superioară | |
| 1 x abaterea standard | 68.3% | 21 | 26 | |
| 2 x abatere standard | 95.5% | 18.5 | 28.5 | |
| 3 x abaterea standard | 99.7% | 16 | 31 |
Cu o probabilitate de 68,3%, durata activității va fi cuprinsă între 21 și 26 de zile. Pentru un interval cuprins între 18,5 și 28,5 zile, probabilitatea este de 95,5%. Utilizarea a 3 abateri standard acoperă aproape în întregime toate punctele de date și determină o probabilitate de 99,7% ca durata să fie în cele din urmă între 16 și 31 de zile.
Rezumat
Stimarea finală în cadrul metodei triunghiulare a fost de 23, comparativ cu 23,5 folosind metoda PERT. Acest lucru se datorează faptului că cea din urmă atribuie o pondere mai mare cazului „cel mai probabil” care, în cazul nostru, nu este exact media (sau media neponderată) a estimării optimiste și a celei pesimiste.
Utilizarea metodei PERT permite luarea în considerare a probabilităților intervalelor de valori. Acest lucru este util în cazul în care calitatea estimărilor variază, de exemplu, dacă diferența dintre estimările optimiste și pesimiste se abate semnificativ între diferite activități. În acest caz, utilizarea intervalelor de valori și a probabilităților acestora va reflecta dispersia și nivelul de încredere al estimărilor subiacente.
Concluzie
Stimarea activităților în ceea ce privește cerințele de timp și de cost ale acestora este crucială pentru planificarea și programarea proiectelor și activităților. În multe proiecte, nu sunt disponibile estimări mai precise, cum ar fi estimările parametrice, bazate pe corelații statistice ale unor proiecte comparabile din trecut, de exemplu. Tehnica de estimare în trei puncte oferă o bună abordare pentru prelucrarea și echilibrarea estimărilor de sus în jos sau a estimărilor experților în domeniu în astfel de situații.
Distribuția PERT este probabil cea mai precisă metodă de agregare a acestor cazuri cele mai rele, cele mai bune și cele mai probabile într-o singură cifră (valoare așteptată) sau într-un interval de valori. Datorită utilizării deviației standard, aceasta ia în considerare atât incertitudinile inerente, cât și potențiala dispersie a estimărilor.
Acesta ar putea fi motivul pentru care PERT este încă o metodă comună în estimarea și programarea proiectelor, deși există de câteva decenii și ar fi putut fi folosită deja de bunicii noștri (dacă ar fi fost manageri de proiect).
.
