Un comparator digital de magnitudine este un circuit combinațional care compară două numere digitale sau binare pentru a afla dacă un număr binar este egal, mai mic sau mai mare decât celălalt număr binar. În mod logic, proiectăm un circuit pentru care vom avea două intrări, una pentru A și alta pentru B și vom avea trei terminale de ieșire, una pentru condiția A > B, una pentru condiția A = B și una pentru condiția A < B.
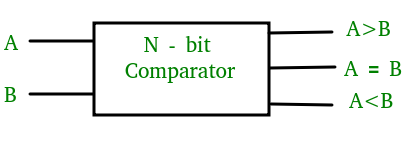
Comparator de mărime 1 bit –
Un comparator folosit pentru a compara doi biți se numește comparator pe un singur bit. Acesta constă din două intrări, fiecare pentru două numere pe un singur bit și trei ieșiri pentru a genera mai mic decât, egal cu și mai mare decât între două numere binare.
Tabelul de adevăr pentru un comparator pe 1 bit este dat mai jos:
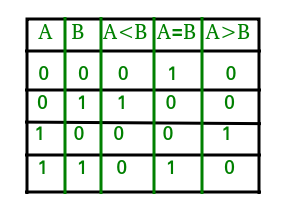
Din tabelul de adevăr de mai sus, expresiile logice pentru fiecare ieșire pot fi exprimate după cum urmează:
A>B: AB'A<B: A'BA=B: A'B' + AB
Din expresiile de mai sus se poate obține următoarea formulă:

Cu ajutorul acestor expresii booleene, putem implementa un circuit logic pentru acest comparator, așa cum este prezentat mai jos:
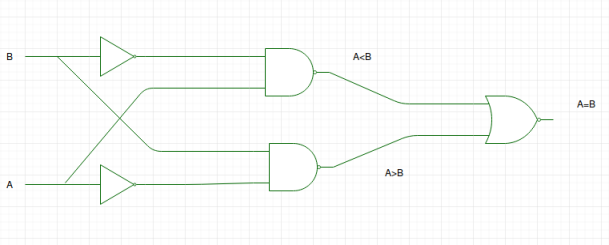
Schema logică este greșită
Comparator de magnitudine pe 2 biți –
Un comparator utilizat pentru a compara două numere binare, fiecare de doi biți, se numește comparator de magnitudine pe 2 biți. Acesta este format din patru intrări și trei ieșiri pentru a genera mai mic decât, egal cu și mai mare decât între două numere binare.
Tabelul de adevăr pentru un comparator pe 2 biți este dat mai jos:
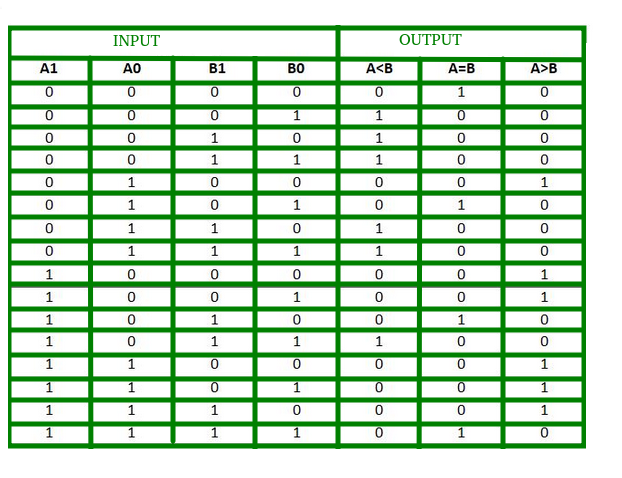
Din tabelul de adevăr de mai sus se poate trasa harta K pentru fiecare ieșire după cum urmează:



Din hărțile K de mai sus se pot exprima expresii logice pentru fiecare ieșire după cum urmează:
A>B:A1B1' + A0B1'B0' + A1A0B0'A=B: A1'A0'B1'B0' + A1'A0B1'B0 + A1A0B1B0 + A1A0'B1B0' : A1'B1' (A0'B0' + A0B0) + A1B1 (A0B0 + A0'B0') : (A0B0 + A0'B0') (A1B1 + A1'B1') : (A0 Ex-Nor B0) (A1 Ex-Nor B1)A<B:A1'B1 + A0'B1B0 + A1'A0'B0
Cu ajutorul acestor expresii booleene, putem implementa un circuit logic pentru acest comparator, așa cum este prezentat mai jos:
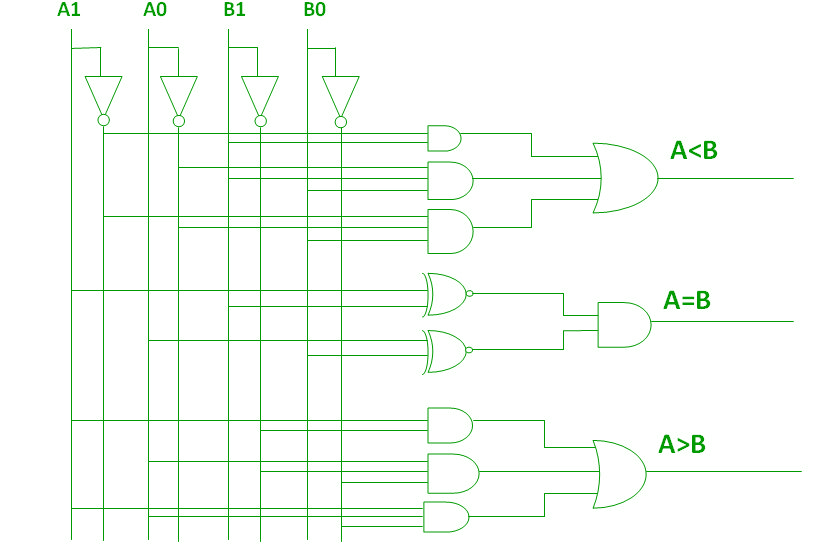
Comparator de magnitudine pe 4 biți –
Un comparator utilizat pentru a compara două numere binare, fiecare de patru biți, se numește comparator de magnitudine pe 4 biți. Acesta este format din opt intrări, fiecare pentru două numere de patru biți și trei ieșiri pentru a genera mai mic decât, egal cu și mai mare decât între două numere binare.
Într-un comparator pe 4 biți condiția de A>B poate fi posibilă în următoarele patru cazuri:
- Dacă A3 = 1 și B3 = 0
- Dacă A3 = B3 și A2 = 1 și B2 = 0
- Dacă A3 = B3, A2 = B2 și A1 = 1 și B1 = 0
- Dacă A3 = B3, A2 = B2 și A1 = 1 și B1 = 0
- Dacă A3 = B3, A2 = B2, A1 = B1 și A0 = 1 și B0 = 0
În mod similar, condiția pentru A<B poate fi posibilă în următoarele patru cazuri:
- Dacă A3 = 0 și B3 = 1
- Dacă A3 = B3 și A2 = 0 și B2 = 1
- Dacă A3 = B3, A2 = B2 și A1 = 0 și B1 = 1
- Dacă A3 = B3, A2 = B2 și A1 = 0 și B1 = 1
- Dacă A3 = B3, A2 = B2, A1 = B1 și A0 = 0 și B0 = 1
Condiția A=B este posibilă numai atunci când toți biții individuali ai unui număr coincid exact cu biții corespunzători ai unui alt număr.
Din afirmațiile de mai sus expresiile logice pentru fiecare ieșire pot fi exprimate după cum urmează:
AA, 831331 r: (A3 EioNor 33)A2132′ a (A3 Ex-Nor 133) (A2 Ex-Nor 132)A131′ a (A3 Ex-Nor 33) (A2 ENor132) (Al Ex-Nor 31)A01301
,13: A3’03 a (A3 Ex-Nor 33)A211:12 a (A3 Ex-Nor 83) (A2 Ex-Nor 132)Ar131 a (A3 Ex-Nor 33) (A2 Ex-Nor32) (Al Ex-Nor 131)A0N30
A=B: (A3 Ex-Nor B3) (A2 Ex-Nor 82) (Al Ex-Nor BI) (AO Ex-Nor BO)
Cu ajutorul acestor expresii booleene, putem implementa un circuit logic pentru acest comparator, așa cum este prezentat mai jos:
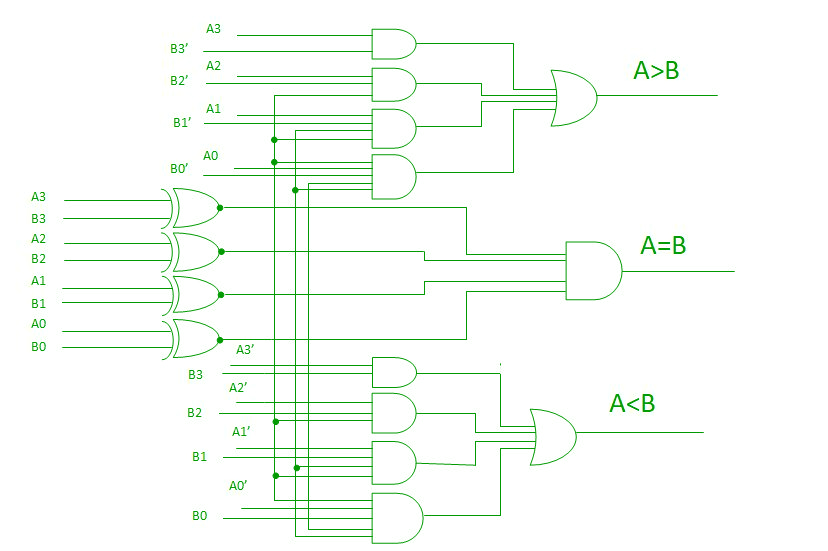
Comparator în cascadă –
Un comparator care efectuează operația de comparare a mai mult de patru biți prin cascadă a două sau mai multe comparatoare pe 4 biți se numește comparator în cascadă. Atunci când două comparatoare trebuie să fie cascadate, ieșirile comparatorului de ordin inferior sunt conectate la intrările corespunzătoare ale comparatorului de ordin superior.
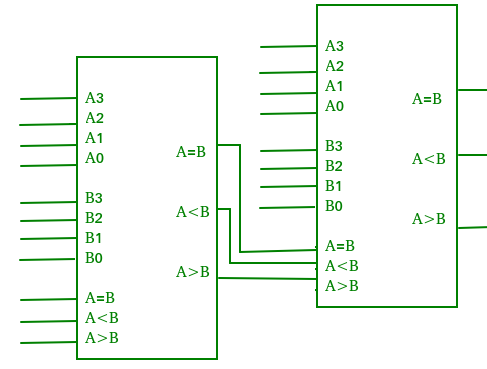
Aplicații ale comparatoarelor –
- Comparatoarele sunt utilizate în unitățile centrale de procesare (CPU) și în microcontrolere (MCU).
- Celea sunt utilizate în aplicații de control în care numerele binare care reprezintă variabile fizice cum ar fi temperatura, poziția etc. sunt comparate cu o valoare de referință.
- Comparatoarele sunt, de asemenea, utilizate ca controlere de proces și pentru controlul servomotoarelor.
- Utilizate în aplicații de verificare a parolelor și biometrice.
