Cu câțiva ani în urmă, Scott Fortmann-Roe a scris un eseu grozav intitulat „Înțelegerea compromisului dintre bias și varianță.”
Pe măsură ce știința datelor se transformă într-o profesie acceptată cu propriul set de instrumente, proceduri, fluxuri de lucru etc., adesea pare să se pună mai puțin accentul pe procesele statistice în favoarea aspectelor mai interesante (a se vedea aici și aici pentru o pereche de exemple de discuții).
Definiții conceptuale
În timp ce aceasta va servi ca o prezentare generală a eseului lui Scott, pe care îl puteți citi pentru mai multe detalii și intuiții matematice, vom începe cu definițiile textuale ale lui Fortmann-Roe, care sunt esențiale pentru lucrare:
Error due to Bias: Eroarea cauzată de părtinire este luată ca diferența dintre predicția așteptată (sau medie) a modelului nostru și valoarea corectă pe care încercăm să o prezicem. Desigur, aveți doar un singur model, astfel încât să vorbiți despre valori de predicție așteptate sau medii poate părea puțin ciudat. Totuși, imaginați-vă că ați putea repeta întregul proces de construire a modelului de mai multe ori: de fiecare dată când adunați date noi și efectuați o nouă analiză, creând un nou model. Din cauza caracterului aleatoriu al seturilor de date subiacente, modelele rezultate vor avea o gamă de predicții. Biasul măsoară cât de departe sunt, în general, predicțiile acestor modele de valoarea corectă.
Error due to Variance: Eroarea datorată varianței este considerată ca fiind variabilitatea predicției unui model pentru un anumit punct de date. Din nou, imaginați-vă că puteți repeta întregul proces de construire a modelului de mai multe ori. Varianța reprezintă cât de mult variază predicțiile pentru un anumit punct între diferitele realizări ale modelului.
În esență, tendința este cât de îndepărtate sunt predicțiile unui model de corectitudine, în timp ce varianța este gradul în care aceste predicții variază între iterațiile modelului.
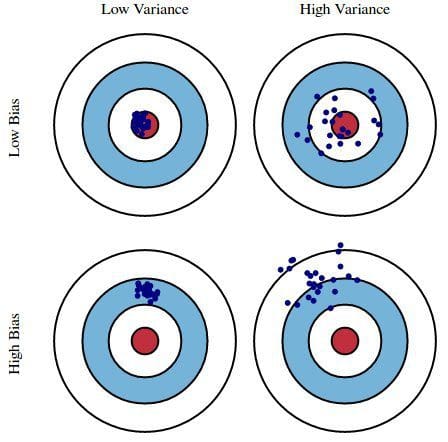
Fig. 1: Ilustrație grafică a bias-ului și varianței
Din Understanding the Bias-Variance Tradeoff, de Scott Fortmann-Roe.
Discuție
Utilizând ca exemplu un sondaj simplu și defectuos pentru alegerile prezidențiale, erorile din sondaj sunt apoi explicate prin prisma celor două lentile ale prejudecății și varianței: selectarea participanților la sondaj dintr-o agendă telefonică este o sursă de prejudecată; o dimensiune mică a eșantionului este o sursă de varianță; minimizarea erorii totale a modelului se bazează pe echilibrarea erorilor de prejudecată și varianță.
Fortmann-Roe continuă apoi să discute aceste probleme în legătură cu un singur algoritm: k-Nearest Neighbor. El oferă apoi câteva aspecte cheie la care trebuie să se gândească atunci când gestionează părtinirea și varianța, inclusiv tehnicile de reeșantionare, proprietățile asimptotice ale algoritmilor și efectul lor asupra erorilor de părtinire și de varianță și lupta împotriva propriilor ipoteze vis-a-vis atât de date, cât și de modelarea acestora.
E eseul se încheie susținând că, în esența lor, aceste 2 concepte sunt strâns legate atât de supra- și subadaptare. În opinia mea, iată care este cel mai important punct:
Pe măsură ce tot mai mulți parametri sunt adăugați la un model, complexitatea modelului crește și varianța devine principala noastră preocupare, în timp ce bias-ul scade constant. De exemplu, cu cât mai mulți termeni polinomiali sunt adăugați la o regresie liniară, cu atât mai mare va fi complexitatea modelului rezultat. Cu alte cuvinte, prejudecata are o derivată de ordinul întâi negativă ca răspuns la complexitatea modelului, în timp ce varianța are o pantă pozitivă.

Fig. 2: Contribuția prejudecății și a varianței la eroarea totală
Din Understanding the Bias-Variance Tradeoff, de Scott Fortmann-Roe.
Fortmann-Roe încheie secțiunea privind supra- și subadaptarea indicând un alt eseu grozav al său (Accurately Measuring Model Prediction Error), trecând apoi la recomandarea extrem de agreabilă conform căreia „măsurile bazate pe reeșantionare, cum ar fi validarea încrucișată, ar trebui să fie preferate măsurilor teoretice, cum ar fi Criteriile de informare ale lui Aikake”.
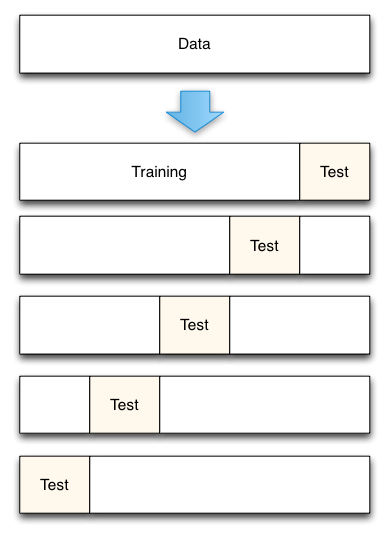
Fig. 3: Divizarea datelor prin validare încrucișată de 5 ori
Din Accurately Measuring Model Prediction Error, de Scott Fortmann-Roe.
Desigur, cu validarea încrucișată, numărul de pliuri de utilizat (validare încrucișată k-fold, nu?), valoarea lui k este o decizie importantă. Cu cât valoarea este mai mică, cu atât mai mare este distorsiunea în estimările erorilor și mai mică este varianța. Dimpotrivă, atunci când k este setat egal cu numărul de instanțe, estimarea erorii este atunci foarte puțin părtinitoare, dar are posibilitatea unei varianțe ridicate. Compromisul prejudecată-varianță este în mod clar important de înțeles chiar și pentru cele mai de rutină metode de evaluare statistică, cum ar fi validarea încrucișată k-fold.
Din păcate, validarea încrucișată pare, de asemenea, uneori, să-și fi pierdut farmecul în epoca modernă a științei datelor, dar aceasta este o discuție pentru altă dată.
Vă recomand să citiți întregul eseu al lui Scott Fortmann-Roe despre compromisul bias-varianță, precum și articolul său despre măsurarea erorii de predicție a modelelor.
Relații:
- Big Data, Bible Codes, and Bonferroni
- Știința datelor de selecție a variabilelor: O trecere în revistă
- Dataets Over Algorithms
