Link State Routing este o tehnică în care fiecare router împărtășește cunoștințele despre vecinătatea sa cu fiecare alt router din rețeaua de internet.
Cele trei chei pentru a înțelege algoritmul Link State Routing:
- Cunoștințe despre vecinătate: În loc să trimită tabelul său de rutare, un router trimite doar informații despre vecinătatea sa. Un router transmite altor routere identitatea și costul legăturilor sale direct atașate.
- Flooding: Fiecare router trimite informațiile către fiecare alt router din rețeaua de internet, cu excepția vecinilor săi. Acest proces este cunoscut sub numele de Flooding. Fiecare router care primește pachetul trimite copii către toți vecinii săi. În cele din urmă, fiecare router primește o copie a aceleiași informații.
- Împărtășirea informațiilor: Un router trimite informația către fiecare alt router numai atunci când are loc o modificare a informației.
Rotingul în starea de legătură are două faze:
Reliable Flooding
- Starea inițială: Fiecare nod cunoaște costul vecinilor săi.
- Starea finală: Fiecare nod cunoaște întregul graf.
Calcularea rutei
Care nod utilizează algoritmul lui Dijkstra pe graf pentru a calcula rutele optime către toate nodurile.
- Algoritmul de rutare în stare de legătură este, de asemenea, cunoscut sub numele de algoritmul lui Dijkstra, care este utilizat pentru a găsi cea mai scurtă cale de la un nod la orice alt nod din rețea.
- Algoritmul lui Dijkstra este un algoritm iterativ și are proprietatea că, după a k-a iterație a algoritmului, cele mai puțin costisitoare căi sunt bine cunoscute pentru k noduri de destinație.
Să descriem câteva notații:
- c( i , j): Costul legăturii de la nodul i la nodul j. Dacă nodurile i și j nu sunt legate direct, atunci c(i , j) = ∞.
- D(v): Definește costul căii de la codul sursă la destinația v care are cel mai mic cost în prezent.
- P(v): Definește nodul anterior (vecinul lui v) împreună cu calea curentă cu cel mai mic cost de la sursă la v.
- N: Este numărul total de noduri disponibile în rețea.
Algoritm
InitializationN = {A} // A is a root node.for all nodes vif v adjacent to Athen D(v) = c(A,v)else D(v) = infinityloopfind w not in N such that D(w) is a minimum.Add w to NUpdate D(v) for all v adjacent to w and not in N:D(v) = min(D(v) , D(w) + c(w,v))Until all nodes in N
În algoritmul de mai sus, un pas de inițializare este urmat de buclă. Numărul de ori de câte ori se execută bucla este egal cu numărul total de noduri disponibile în rețea.
Să înțelegem printr-un exemplu:
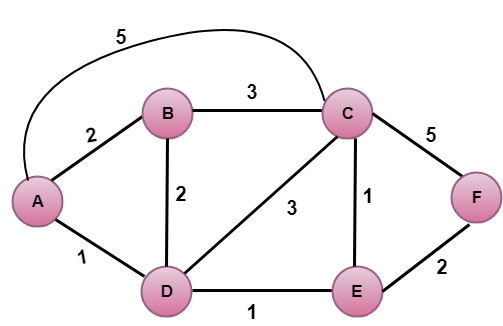
În figura de mai sus, vertexul sursă este A.
Etapa 1:
Prima etapă este o etapă de inițializare. Drumul cel mai puțin costisitor cunoscut în prezent de la A la vecinii săi direct atașați, B, C, D sunt 2,5,1, respectiv. Costul de la A la B este setat la 2, de la A la D este setat la 1, iar de la A la C este setat la 5. Costul de la A la E și F se stabilește la infinit, deoarece acestea nu sunt direct legate de A.
| Step | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | ||
|---|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 5,A | 1,A | ∞ | ∞ | ∞ |
Etapa 2:
În tabelul de mai sus, observăm că vertexul D conține calea cu cel mai mic cost din etapa 1. Prin urmare, acesta este adăugat în N. Acum, trebuie să determinăm cea mai puțin costisitoare cale prin vertexul D.
a) Calcularea celei mai scurte căi de la A la B
b) Calcularea celei mai scurte căi de la A la C
c) Calcularea celei mai scurte căi de la A la E
Nota: Vertexul D nu are o legătură directă cu vertexul E. Prin urmare, valoarea lui D(F) este infinită.
| Step | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | |
|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | ∞ |
| 2 | AD | 2,A | 4,D | 2,D | ∞ |
Etapa 3:
În tabelul de mai sus, observăm că atât E cât și B au calea cu cel mai mic cost în etapa 2. Să luăm în considerare vertexul E. Acum, determinăm cea mai puțin costisitoare cale a celorlalte vârfuri prin E.
a) Calcularea celei mai scurte căi de la A la B.
b) Calcularea celei mai scurte căi de la A la C.
c) Calcularea celei mai scurte căi de la A la F.
| Step | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | |
|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | ||
| 3 | ADE | 2,A | 3,E | 4,E |
Etapa 4:
În tabelul de mai sus, observăm că vertexul B are calea cu cel mai mic cost în etapa 3. Prin urmare, este adăugat în N. Acum, determinăm cea mai puțin costisitoare cale a celorlalte vârfuri prin B.
a) Calcularea celei mai scurte căi de la A la C.
b) Calcularea celei mai scurte căi de la A la F.
| Step | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | |
|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | ||
| 3 | ADE | 2,A | 3,E | 4,E | |||
| 4 | ADEB | 3,E | 4,E |
Etapa 5:
În tabelul de mai sus, observăm că vertexul C are calea cu cel mai mic cost în etapa 4. Prin urmare, acesta este adăugat în N. Acum, determinăm calea cu cel mai mic cost a celorlalte vârfuri prin C.
a) Calcularea celei mai scurte căi de la A la F.
| Etapa | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | |||
|---|---|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | |||
| 2 | AD | 2,A | 4,D | 2,D | ∞ | ||||
| 3 | ADE | 2,A | 3,E | 4,E | |||||
| 4 | ADEB | ADE | 3,E | 4,E | |||||
| 5 | ADEBC | 4,E |
Tabel final:
| Step | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | ||
|---|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | ||
| 2 | AD | 2,A | 4,D | 2,D | ∞ | |||
| 3 | ADE | 2,A | 3,E | 4,E | ||||
| 4 | ADEB | 3,E | 4,E | |||||
| 5 | ADEBC | 4,E | ||||||
| 6 | ADEBCF |
Dezvantaj:
Se creează un trafic intens în rutarea în stare de linie din cauza Flooding-ului. Flooding-ul poate cauza o buclă infinită, această problemă poate fi rezolvată prin utilizarea câmpului Time-to-leave
.
