Introducere :
Similitudinea cosinusoidală este utilizată pentru a determina similaritatea dintre documente sau vectori. Din punct de vedere matematic, măsoară cosinusul unghiului dintre doi vectori proiectați într-un spațiu multidimensional. există și alte tehnici de măsurare a similarității, cum ar fi distanța euclidiană sau distanța Manhattan, dar noi ne vom concentra aici pe similaritatea cosinusului și distanța cosinusului.
Relația dintre similaritatea cosinusului și distanța cosinusului poate fi definită după cum urmează:
- Similaritatea scade atunci când distanța dintre doi vectori crește

2. Similaritatea crește atunci când distanța dintre doi vectori scade.

Similitudinea cosinusală și distanța cosinusală:
Similitudinea cosinusală spune că pentru a afla asemănarea dintre două puncte sau vectori trebuie să găsim unghiul dintre ei.
Formula pentru a găsi similitudinea și distanța cosinusului este cea de mai jos:


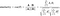
Aici A=punctul P1,B=punctul P2 (în exemplul nostru)
Să vedem diferitele valori ale lui Cos Θ pentru a înțelege similitudinea cosinusului și distanța cosinusului între două puncte de date (vectori) P1 & P2 luând în considerare două axe X și Y.
Imaginea de mai jos având acolo Cazuri.
Cazul 1: Când unghiul dintre punctele P1 & P2 este de 45 de grade atunci
cosine_similaritate= Cos 45 = 0.525
Cazul 2: Când două puncte P1 & P2 sunt departe unul de celălalt și unghiul dintre puncte este de 90 de grade atunci
cosine_similaritate= Cos 90 = 0
Cazul 3: Atunci când două puncte P1 & P2 sunt foarte apropiate și se află pe aceeași axă unul față de celălalt, iar unghiul dintre puncte este de 0 grade, atunci
cosine_similarity= Cos 0 = 1

Imaginea de mai jos conține următoarele trei cazuri.
Cazul 4: Când punctele P1 & P2 sunt opuse unul față de celălalt și iar unghiul dintre puncte este de 180 de grade atunci
cosin_similaritate= Cos 180 = -1
Cazul 5: Când unghiul dintre punctele P1 & P2 este de 270 de grade atunci
cosin_similaritate= Cos 270 = 0
Cazul 6: Când unghiul dintre punctele P1 & P2 este de 270 de grade atunci
cosin_similaritate= Cos 270 = 0
Cazul 6: Când unghiul dintre punctele P1 & P2 este de 360 de grade atunci
cosine_similarity= Cos 360 = 1

Să trecem aceste valori ale fiecărui unghi discutat mai sus și să vedem distanța Cosine între două puncte.
1 – Cosinus_Similaritate=Distanța Cosinusului
Cazul 1: Când Cos 45 de grade
Să înlocuim valorile în formula de mai sus .
1-0.525= Cosine_Distance
0.475 =Cosine_Distance
Cazul 2: Când Cos 90 Degree
1-0= Cosine_Distance
1 =Cosine_Distance
Cazul 3: Când Cos 0 Degree
1-1= Cosine_Distance
0 =Cosine_Distance
Cazul 4: Când Cos 0 Degree
1-1= Cosine_Distance
0 =Cosine_Distance
: Când Cos 180 Degree
1-(-1)= Cosine_Distance
2 =Cosine_Distance
Cazul 5: Când Cos 270 Degree
1-0= Cosine_Distance
1 =Cosine_Distance
1 =Cosine_Distance
Cazul 6: Când Cos 270 Degree
1-0= Cosine_Distance
1 =Cosine_Distance
Cazul 6: Atunci când Cos 360 Degree
1-1= Cosine_Distance
0 =Cosine_Distance
Vezi clar că atunci când distanța este mai mică, similitudinea este mai mare (punctele sunt apropiate unul de celălalt), iar dacă distanța este mai mare, două puncte sunt diferite (îndepărtate unul de celălalt)
Similitudinea Cosine și distanța Cosine sunt foarte utilizate în sistemele de recomandare pentru a recomanda produse utilizatorilor în funcție de ceea ce le place și ceea ce nu le place.
Câteva exemple în care acest lucru este utilizat sunt site-uri web precum Amazon, Flipkart pentru a recomanda articole clienților pentru o experiență personalizată, evaluarea și recomandarea filmelor etc.
Concluzie : Sper că până acum ați înțeles clar matematica din spatele calculului similarității cosinusului și a distanței cosinusului și a utilizării sale.
Sper că vă place articolul meu. vă rog să apăsați Clap 👏 (de 50 de ori) pentru a mă motiva să scriu în continuare.
Vreți să vă conectați :
Linked In : https://www.linkedin.com/in/anjani-kumar-9b969a39/
Dacă vă plac postările mele aici pe Medium și ați dori să continui să fac această muncă, luați în considerare să mă susțineți pe patreon
.
