Aceasta este uneori numită teoria mareelor „statice”, o teorie care a apărut pentru prima dată în faimoasele Principia ale lui Isaac Newton. După ce a identificat forțele care produc mareele, Newton, și alții care l-au urmat, au conceput un ipotetic ocean global în echilibru static cu aceste forțe – un echilibru care cerea un sferoid de apă care să acopere pământul. „Prolat” înseamnă că sfera în cauză a fost întinsă de-a lungul unei linii care unește doi poli; nu polii geografici în acest caz, ci polii aliniați cu corpul ceresc (luna sau soarele), ceea ce determină deformarea sferei oceanice ipotetice. Dacă ne uităm din nou la graficul care ilustrează forțele de tracțiune din modulul anterior, ne putem imagina cu ușurință că apa converge spre acești poli pentru a produce „umflături de maree” gemene – termeni care sunt încă foarte populari în manualele din zilele noastre.
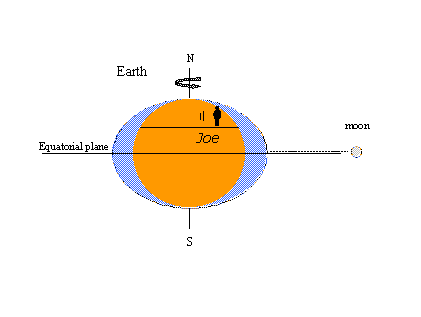
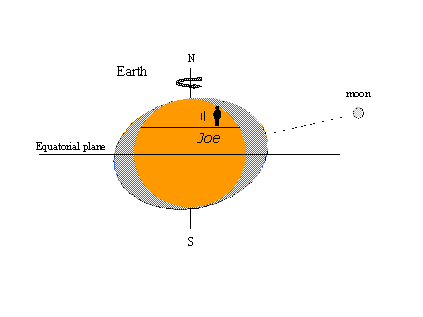
Motivul popularității teoriei echilibrului – cel puțin a conceptului de umflături de maree – este că este ușor de explicat anumite fenomene de maree bine cunoscute cu ajutorul imaginilor. În cea din stânga de mai jos, un observator imaginar pe nume Joe se rotește cu Pământul și întâlnește umflăturile statice sub forma mareelor mari.Ori de câte ori luna traversează meridianul local al lui Joe, el este martor la maree maree. Este din nou maree înaltă douăsprezece ore lunare mai târziu, când luna traversează meridianul opus de pe cealaltă parte a pământului. Două maxime și două minime au loc într-o singură zi lunară care durează 24 de ore și 50 de minute în timpul de ceas (solar). În figura din dreapta, luna a progresat pe orbita sa în jurul pământului până la o poziție la nord de ecuator (declinație nordică). Umflăturile statice se deplasează pentru a se menține în linie cu luna și acum Joe întâlnește o inegalitate diurnă a mareelor înalte (maree înalte succesive de înălțime inegală). Declinația lunară maximă, la nord sau la sud de ecuator, produce maree tropice; mareele care se produc atunci când luna se află pe ecuator se numesc maree ecuatoriale. mareele tropice-ecuatoriale se repetă de două ori într-un interval de 27 1/3 zile – luna tropică acoperind un ciclu complet în declinația lunară. Toate acesteobservații sunt în concordanță cu teoria echilibrului.
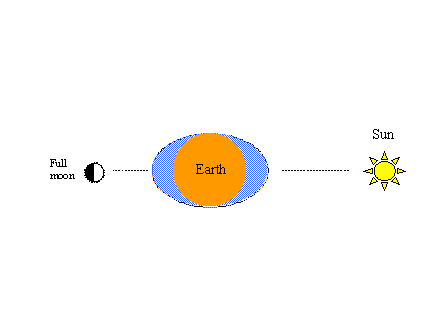
Un alt fenomen ușor de demonstrat în acest fel este binecunoscutul ciclu primăvară-primăvară. Gravitația solară produce, de asemenea, o pereche de umflături de mare în oceanul ipotetic. Atunci când forțele de tracțiune ale Soarelui și ale Lunii sunt aliniate, rezultă maree de primăvară cu o amplitudine mai mare (maxime mai mari și minime mai mici)așa cum se arată în figura din stânga de mai jos. La fel ca în figurile anterioare,când luna completează o altă jumătate de ciclu pe orbita sa – de data aceasta de la lună plină la lună nouă – se vor produce din nou maree de primăvară.
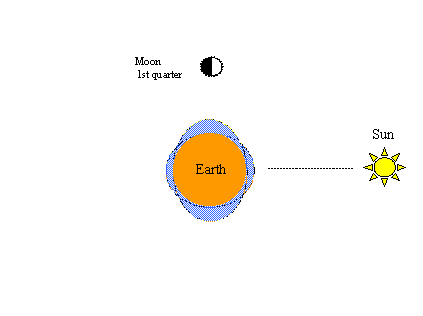
Figura de mai jos din dreapta ilustrează porțiunea de primăvară-maree a ciclului de primăvară-maree; adică atunci când luna se află în primul sfert (sau al treilea sfert) al acelui ciclu, forțele de tracțiune lunară și solară sunt complet nealiniate, având tendința de a se contracara reciproc, și rezultă maree de primăvară cu amplitudine mai mică (maxime mai mici și minime mai mari). Două cicluri primăvară-maree (două primăveri șidouă minime) se încheie în 29 ½ zile, aceeași perioadă de timp necesară pentru ca Luna să parcurgă o orbită completă a Pământului în raport cu Soarele.
Alte aspecte ale mareei observate în concordanță cu teoria echilibrului includ ciclul perigeu-apogeu. Acesta provine din faptul că orbita lunii în jurul pământului descrie o elipsă mai degrabă decât un cerc. Mareele perigeene, cu rază de acțiune mai mare, au loc la perigeul lunar, când luna se află cel mai aproape de pământ, iar mareele apogeene, cu rază de acțiune mai mică, au loc la apogeul lunar, când luna se află cel mai departe de pământ pe orbita sa eliptică. Ciclul perigeu-apogean are nevoie de aproximativ 27 ½ zile pentru a se completa.
Deși teoria echilibrului face o treabă excelentă în explicarea fenomenelor ciclice ale mareelor și a perioadelor de recurență asociate cu multe dintre ele, ea este un exemplu de model de comportament ideal – ceva care funcționează pentru scopul propus, deși s-ar putea să nu adere la adevăr în toate situațiile. Nu trebuie să căutăm prea departe acele cazuri. Pământul este acoperit doar parțial de apele sale, masele de uscat împiedică orice lucru care seamănă cu o abulie să se deplaseze complet în jurul său, iar observațiile asupra mareelor reale arată că acestea nu răspund instantaneu la forțele de producere a mareelor de către Lună și Soare, așa cum cere teoria.
