För att addera (eller subtrahera) bråk krävs att bråkens nämnare är lika stora.
Lika stora nämnare
Om nämnarna är lika stora beräknas summan av bråken genom att addera täljarna och behålla nämnaren.
Exempel:
Låt oss addera 4/7 och 3/7:
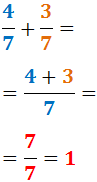På samma sätt beräknas subtraktion av bråk med lika stora nämnare genom att subtrahera täljaren och behålla nämnaren.
Exempel:
Vi subtraherar 4/7 och 3/7:
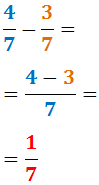
Olika nämnare
När nämnarna är olika måste vi operera lite för att ändra bråken till likvärdiga bråk så att de har samma nämnare.
Låt oss förklara hur vi räknar ut summan
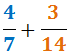
1. Vi beräknar den minsta gemensamma multipeln av nämnarna:
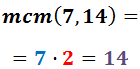
2. I nämnaren för varje bråk skriver vi den minsta gemensamma multipeln som erhållits:
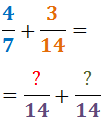
3. I täljaren för varje bråk skriver vi resultatet av att dividera den minsta gemensamma multipeln (den nya nämnaren) med den ursprungliga nämnaren och multiplicera den med den ursprungliga täljaren: Den ursprungliga nämnaren för det första bråket var 7 och den ursprungliga täljaren var 4:
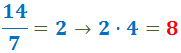
Den ursprungliga nämnaren för det andra bråket var 14 och den ursprungliga täljaren var 3:
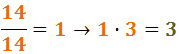
Därmed har vi summan av två bråk med samma nämnare:
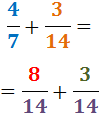
4. Vi adderar bråken:
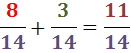
För att subtrahera följer vi samma steg, men på slutet subtraherar vi bråken istället för att addera dem.
Fraktionsresurser:
- Begreppet bråk
- Förenkla bråk
- Ekvivalenta bråk (1)
- Ekvivalenta bråk (2)
- Addera och subtrahera bråk
- Multiplicera och dividera. bråk
- Fraktgenerering av decimaltal
- Blandade bråk
- Procentproblem
- Interaktiva bråkövningar
- Operationer med bråk