Introduktion :
Kosinläget används för att bestämma likheten mellan dokument eller vektorer. Matematiskt sett mäter den cosinus av vinkeln mellan två vektorer som projiceras i ett flerdimensionellt rum.Det finns andra tekniker för att mäta likhet, t.ex. euklidisk distans eller Manhattan-distans, men vi kommer här att fokusera på cosinuslikhet och cosinusavstånd.
Sambandet mellan cosinuslikhet och cosinusavstånd kan definieras enligt följande:
- Likheten minskar när avståndet mellan två vektorer ökar

2. Likheten ökar när avståndet mellan två vektorer minskar.

Cosinuslikhet och Cosinusavstånd:
Cosinuslikhet säger att för att hitta likheten mellan två punkter eller vektorer måste vi hitta vinkeln mellan dem.
Formeln för att hitta Cosinus likhet och avstånd är som nedan:


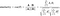
Här A=Punkt P1,B=Punkt P2 (i vårt exempel)
Låt oss se de olika värdena för Cos Θ för att förstå cosinuslikhet och cosinusavstånd mellan två datapunkter (vektorer) P1 & P2 med hänsyn till de två axlarna X och Y.
Understående bild har olika fall.
Fall 1: När vinkeln mellan punkterna P1 & P2 är 45 grader så
cosine_similarity= Cos 45 = 0.525
Fall 2: När två punkter P1 & P2 ligger långt ifrån varandra och vinkeln mellan punkterna är 90 grader så
cosine_similarity= Cos 90 = 0
Fall 3: När två punkter P1 & P2 är mycket nära varandra och ligger på samma axel och vinkeln mellan punkterna är 0 grader så
cosine_similarity= Cos 0 = 1

Nedan visas en bild med de tre följande fallen.
Fall 4: När punkterna P1 & P2 ligger mittemot varandra och vinkeln mellan punkterna är 180 grader så
cosine_similarity= Cos 180 = -1
Fall 5: När vinkeln mellan punkterna P1 & P2 är 270 grader så
cosine_similarity= Cos 270 = 0
Fall 6: När vinkeln mellan punkterna P1 & P2 är 360 grader så
cosine_similarity= Cos 360 = 1

Låt oss passera dessa värden för varje vinkel som diskuterats ovan och se cosinusavståndet mellan två punkter.
1 – Cosine_Similarity=Cosine_Distance
Fall 1: När Cos 45 Degree
Låt oss ersätta värdena i ovanstående formel .
1-0.525= Cosine_Distance
0.475 =Cosine_Distance
Fall 2: När Cos 90 Degree
1-0= Cosine_Distance
1 =Cosine_Distance
Fall 3: När Cos 0 Degree
1-1= Cosine_Distance
0 =Cosine_Distance
Fall 4: När Cos 180 Degree
1-(-1)= Cosine_Distance
2 =Cosine_Distance
Fall 5: När Cos 270 Degree
1-0= Cosine_Distance
1 =Cosine_Distance
Fall 6: När Cos 360 Degree
1-1= Cosine_Distance
0 =Cosine_Distance
Vi kan tydligt se att när avståndet är mindre är likheten större (punkterna är nära varandra) och när avståndet är större är två punkter olikartade (långt ifrån varandra)
Cosine Likhet och Cosine Avstånd används flitigt i rekommendationssystem för att rekommendera produkter till användarna baserat på vad de gillar och inte gillar.
Få exempel där detta används är webbplatser som Amazon och Flipkart för att rekommendera varor till kunderna för en personlig upplevelse, filmer som betygsätts och rekommenderas osv.
Slutsats: Jag hoppas att du nu har en klar förståelse för matematiken bakom beräkningen av cosinuslikhet och cosinusavstånd och dess användning.
Hoppar att du gillar min artikel.Tryck gärna på Clap 👏(50 gånger) för att motivera mig att skriva vidare.
Vill du ansluta :
Linked In : https://www.linkedin.com/in/anjani-kumar-9b969a39/
Om du gillar mina inlägg här på Medium och vill att jag ska fortsätta att göra detta arbete, kan du överväga att stödja mig på patreon
.
