At addere (eller subtrahere) brøker kræver, at brøkenes nævner er lige store.
Lige nævner
Hvis nævnerne er lige store, beregnes summen af brøkerne ved at addere tællerne og beholde nævneren.
Eksempel:
Lad os lægge 4/7 og 3/7 sammen:
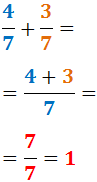 På samme måde beregnes subtraktion af brøker med samme nævner ved at trække tællerne fra hinanden og beholde nævneren.
På samme måde beregnes subtraktion af brøker med samme nævner ved at trække tællerne fra hinanden og beholde nævneren.
Eksempel:
Vi subtraherer 4/7 og 3/7:
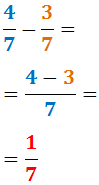
Differente nævner
Når nævnerne er forskellige, skal vi operere lidt for at ændre brøkerne til ækvivalente brøker, så de har den samme nævner.
Lad os forklare proceduren, mens vi beregner summen
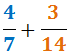
1. Vi beregner det mindste fælles multiplum af nævnerne:
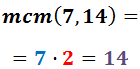
2. I nævneren af hver brøk skriver vi det mindste fælles multiplum, der er opnået:
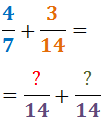
3. I tælleren af hver brøk skriver vi resultatet af at dividere det mindste fælles multiplum (den nye nævner) med den oprindelige nævner og gange det med den oprindelige tæller: Den oprindelige nævner i den første brøk var 7, og den oprindelige tæller var 4:
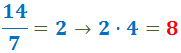
Den oprindelige nævner for den anden brøk var 14, og den oprindelige tæller var 3:
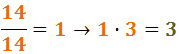
Dermed har vi summen af to brøker med samme nævner:
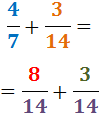
4. Vi lægger brøkerne sammen:
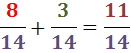
For at trække fraktionerne fra hinanden følger vi de samme trin, men til sidst trækker vi dem fra hinanden i stedet for at lægge brøkerne sammen.
Ressourcer til brøker:
- Begreb om brøker
- Forenkling af brøker
- Ekvivalente brøker (1)
- Ekvivalente brøker (2)
- Tilføje og subtrahere brøker
- Multiplikere og dividere. brøker
- Brøker, der genererer decimaltal
- Blandede brøker
- Procentvise opgaver
- Interaktive brøkøvelser
- Operationer med brøker
