Anvendelse af Buckingham Pi-sætningen

Næste: Betydningen af ikke-dimensionelle tal Op: Buckingham Pi-sætning Forrige: Buckingham Pi-sætning

Anvendelse af Buckingham Pi-sætning

Den sætning, vi har anført, er meget generel, men på ingen måde begrænset til væskemekanikken. Det anvendes inden for mange forskellige områder som f.eks. botanik og samfundsvidenskab, og der er skrevet bøger og bind om dette emne. Men vi har ikke brug for meget teori for at kunne anvende det. Det, vi vil overveje, er en fremgangsmåde til at anvende teoremet og nå frem til ikke-dimensionale tal for en given strømning.

1. Listen over alle de variabler, der styrer processen. Disse variabler skal være uafhængige af hinanden. Man bør f.eks. ikke vælge densitet, tyngdekraft og specifik vægt. Massefylde og specifik vægt bør være tilstrækkeligt. I vores opgave har vi F, D, V, og . Vi har n = 5.
2. Mærk de gentagende variabler. I vores tilfælde er disse D, V og , hvilket giver k = 3 .
3. Beslut, hvor mange ikke-dimensionale tal der er. I vores tilfælde har vi n – k = 2. Vores opgave har 2 ikke-dimensionale tal, og .
4. Definér de ikke-dimensionale tal ved at gruppere variablerne i n – k grupper, således at hver gruppe har alle de gentagne variabler og en ikke-repeterende variabel. For vores problem har vi således

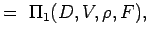
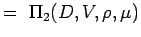
   		(5.2)
   Let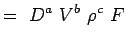
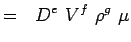
   		(5.3)

5. Udtryk nu hver enkelt variabel i form af dens dimensioner. Lad os anvende MLT-systemet, hvorefter variablerne for voresproblemer har følgende dimensioner.
   

   Variabel	Dimensioner
   F, Kraft	M L / T2 eller M L T-2
   D, Diameter:	L
   V, Hastighed	L/T eller LT-1
   , Massefylde:	M/L3 eller ML-3
   , Viskositet	ML-1T-1

   Substituerer man disse dimensioner i Eqn. 5.2, har vi

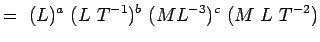
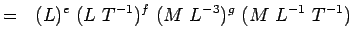
   		(5.4)
   Og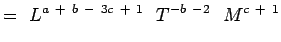
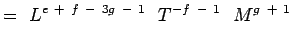
   		(5.5)

   Som følge af, at og er ikke-dimensionale, har vi,

   a + b – 3c + 1 = 0; -b – 2 = 0, c + 1 = 0
   e + f – 3g – 1 = 0; -f – 1 = 0;g + 1 = 0	(5.6)

   Løsning af ligningerne giver,

   a = -2, b = -2, c = -1
   e = -1, f = -1, g = -1	(5.7)

   Nu bliver vores ikke-dimensionale tal,

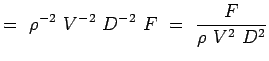
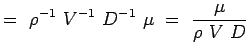
   		(5.8)

Sådan har vi fundet de ikke-dimensionelle tal for den strømning, der er af interesse, nemlig trækket om en cirkulær cylinder. Den funktionelle sammenhæng mellem de to tal kan udtrykkes som

Men bemærk, at den form for udtrykket , som vi har udledt, er noget anderledes end det, vi antog i begyndelsen. Den højre side af ligningen er faktisk den inverse af Reynoldstallet!Dette peger på den ulempe ved analysen, at den nøjagtige funktionelle form mellem -tallene ikke kan opnås. Enhver koefficient eller ethvert indeks, der opnås, kan ikke bestemmes ved denne analyse. Det bør bestemmes ved forsøg eller ved beregninger. Men da tallene er ikke-dimensionelle, kan vi i stedet skrive,

næste: Betydningen af ikke-dimensionelle tal Op: Buckingham Pi-sætning Forrige: Buckingham Pi-sætning

(c) Aerospace, Mechanical & Mechatronic Engg. 2005
University of Sydney