Introduktion :
Cosinus lighed bruges til at bestemme ligheden mellem dokumenter eller vektorer. Matematisk set måler den cosinus af vinklen mellem to vektorer projiceret i et flerdimensionalt rum.Der findes andre similaritetsmålingsteknikker som f.eks. euklidisk afstand eller Manhattan-afstand, men vi vil her fokusere på cosinuslignende lighed og cosinusafstand.
Sammenhængen mellem cosinus lighed og cosinus afstand kan defineres som nedenfor.
- Lighed mindskes, når afstanden mellem to vektorer øges

2. Ligheden øges, når afstanden mellem to vektorer mindskes.

Cosinus lighed og cosinus afstand:
Cosinus lighed siger, at for at finde ligheden mellem to punkter eller vektorer skal vi finde vinklen mellem dem.
Formel til at finde cosinus lighed og afstand er som nedenfor:


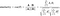
Her A=Punkt P1,B=Punkt P2 (i vores eksempel)
Lader os se de forskellige værdier af Cos Θ for at forstå cosinus lighed og cosinus afstand mellem to datapunkter (vektorer) P1 & P2 under hensyntagen til to akser X og Y.
Nedenstående billede har der tilfælde.
Fælde 1: Når vinklen mellem punkterne P1 & P2 er 45 grader, så
cosine_similarity= Cos 45 = 0.525
Fælde 2: Når to punkter P1 & P2 er langt fra hinanden, og vinklen mellem punkterne er 90 grader, så
cosine_similarity= Cos 90 = 0
Fælde 3: Når to punkter P1 & P2 er meget tæt på hinanden og ligger på samme akse og vinklen mellem punkterne er 0 grader, så
cosine_similarity= Cos 0 = 1

Understående billede viser de næste tre tilfælde.
Fælde 4: Når punkterne P1 & P2 ligger over for hinanden og vinklen mellem punkterne er 180 grader, så
cosine_similarity= Cos 180 = -1
Fælde 5: Når vinklen mellem punkterne P1 & P2 er 270 grader, så
cosine_similarity= Cos 270 = 0
Fælde 6: Når vinklen mellem punkterne P1 & P2 er 360 grader så
cosine_similarity= Cos 360 = 1

Lader os passere disse værdier af hver vinkel diskuteret ovenfor og se Cosine afstanden mellem to punkter.
1 – Cosinus_Similarity=Cosine_Distance
Fald 1: Når Cos 45 Degree
Lader os erstatte værdierne i ovenstående formel .
1-0.525= Cosine_Distance
0.475 =Cosine_Distance
Case 2: Når Cos 90 Degree
1-0= Cosine_Distance
1 =Cosine_Distance
Case 3: Når Cos 0 Degree
1-1= Cosine_Distance
0 =Cosine_Distance
Case 4: Når Cos 180 Grad
1-(-1)= Cosine_Distance
2 =Cosine_Distance
Fælde 5: Når Cos 270 Grad
1-0= Cosine_Distance
1 =Cosine_Distance
Fælde 6: Når Cos 270 Grad
1 =Cosine_Distance
: Når Cos 360 Degree
1-1= Cosine_Distance
0 =Cosine_Distance
Vi kan tydeligt se, at når afstanden er mindre, er ligheden større (punkterne er tæt på hinanden), og når afstanden er større, er to punkter ulige (langt væk fra hinanden)
Cosine Similarity og Cosine Distance anvendes i høj grad i anbefalingssystemer til at anbefale produkter til brugerne på grundlag af deres smag og ubehag.
Få eksempler på, hvor dette bruges, er websteder som Amazon og Flipkart til at anbefale varer til kunderne for at give dem en personlig oplevelse, filmvurdering og anbefaling osv.
Konklusion : Jeg håber, at du nu har en klar forståelse af matematikken bag beregningen af cosinus lighed og cosinus afstand og dens brug.
Håber du kan lide min artikel.Tryk venligst på Clap 👏(50 gange) for at motivere mig til at skrive videre.
Vil du oprette forbindelse :
Linked In : https://www.linkedin.com/in/anjani-kumar-9b969a39/
Hvis du kan lide mine indlæg her på Medium og ønsker, at jeg skal fortsætte med dette arbejde, så overvej at støtte mig på patreon
